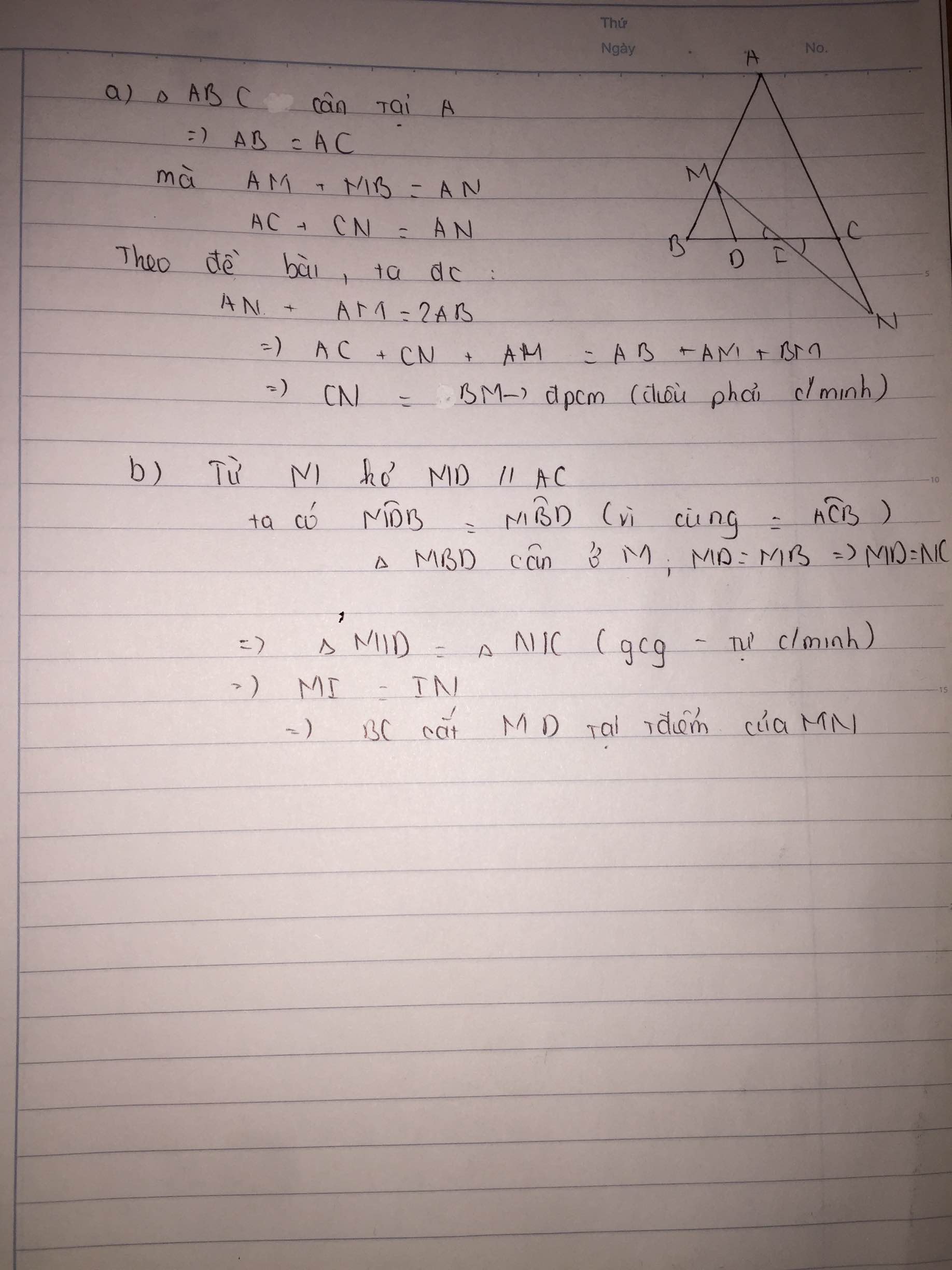Giups mk nha! Mk cần gấp lắm!
Cho tam giác ABC cân tại A. Trên AB lấy M, trên tia đối của tia CA lấy N sao cho AM +AN = 2AB.
a) CM: BM = CN
b) CM: BC đi qua trung điểm của MN
c) Đường trung trực MN và tia phân giác của BAC cắt nhau tại K. CM: KC vuông góc AC