Một người nông dân đến gặp nhà vua và khẩn cầu : -" Kính mong hoàng đế tối cao, ngài hãy cho kẻ hạ thần này xin 1 quả táo trong vườn của ngài". Nhà vua chấp nhận. Ngừơi nông dân đi vào vườn và thấy: Toàn bộ vườn của nhà vua được rào bằng ba lớp. Mỗi lớp rào chỉ có 1 cổng ra vào và cạnh mỗi cổng ra vào là 1 người lính gác . Anh ta đến gặp người lính gác và nói: -"Nhà vua đồng ý cho tôi lấy 1 quả táo". -"Anh cứ vào lấy nhưng khi ra anh phải đưa tôi một nữa số táo lấy dược và thêm 1 quả".Người lính gác thứ nhất nói. Lời nói đó được lặp lại cho đến khi gặp người ính gác thứ hai và thứ ba. Hồi xưa cũng có tham nhũng đó nha:01 :01 :p :p Hỏi ngừơi nông dân phải lấy bao nhiêu quả để khi ra khỏi lớp rào anh ta chỉ còn đúng 1 quả.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số táo cần hái được là a
Khi ra cổng 1 phải cho \(\frac{a}{2}\)+ 1 và còn \(\frac{a}{2}\) - 1
qua cổng 2 phải cho : \(\frac{1}{2}\)(\(\frac{a}{2}\)-1) +1 = \(\frac{a}{4}\) - \(\frac{1}{2}\)+ 1 = \(\frac{a}{4}\)+ \(\frac{1}{2}\)
vậy còn lại:( \(\frac{a}{2}\)- 1) - (\(\frac{a}{4}\)+ \(\frac{1}{2}\)) = \(\frac{a}{4}\) - \(\frac{3}{2}\)
Qua cổng 3 phải cho: \(\frac{1}{2}\).(\(\frac{a}{4}\)-\(\frac{3}{2}\)) +1 = \(\frac{a}{8}\)-\(\frac{3}{4}\)+ 1 = \(\frac{a}{8}\)+ \(\frac{1}{4}\)
vậy còn lại: (\(\frac{a}{4}\)- \(\frac{3}{2}\))- (\(\frac{a}{8}\) + \(\frac{1}{4}\)) = \(\frac{a}{8}\)- \(\frac{7}{4}\) và bằng 1 quả =>
\(\frac{a}{8}\)= 1+\(\frac{7}{4}\)= \(\frac{11}{4}\) => a = 22 (quả)

Với một hình chữ nhất có chu vi không đổi thì diện tích của nó là lớn nhất khi nó là hình vuông.
Chứng minh điều này có thể phải dùng tới kiến thức về bất đẳng thức ở cấp II.
Chứng minh:
Gọi chiều dài hình chữ nhật là a; chiều rộng hình chữ nhật là b; Chi vi hình chữ nhật là C.
Ta có: \(C=2\left(a+b\right)\)
Diện tích hình chữ nhật là:\(S=a.b\)
Mà: \(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2+2ab-4ab\ge0\Rightarrow\left(a+b\right)^2\ge4ab\Rightarrow ab\le\frac{\left(a+b\right)^2}{4}\)
\(\Rightarrow S=ab\le\frac{\left(a+b\right)^2}{4}=\frac{\left(\frac{C}{2}\right)^2}{4}=\frac{C^2}{16}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\) hay chiều dài = chiều rộng, hay hình chữ nhật là hình vuông.
Vậy bác nông dân khoanh mảnh đất thành hình vuông thì sẽ nhận được diện tích lớn nhất (có lợi nhất).
Bài toán có thể hiểu là: Trong các hình: tròn, vuông và hình chữ nhật cùng chu vi, xét xem hình nào có diện tích lớn nhất. Ta so sánh diện tích các hình trên qua đại lượng chu vi . Gọi chu vi ( độ dài sợ dây) là C; ta có:
Svuông= C/4 xC/4= CxC/16. Để biến hình vuông thành hình chữ nhật thì phải bớt cạnh này của hình vuông và thêm vào cạnh kia của hình vuông một lượng, chẳng hạn là a, ta có chiều dài là C/4+a và chiều rộng là C/4-a; khi đó diện tích hình chữ nhật là
Schữ nhật= (C/4+a)x(C/4-a)= CxC/16- axa , vì là hình chữ nhật nên a>0, nên Schữ nhât < Svuông.
Ta lại có Stròn=3,14xCxC/4x3,14x3,14 = CxC/4x3,14 > CxC/16 Vậy Stròn> Svuông> Schữ nhật..
Kết luận: Nếu hình tròn, hình vuông và hình chữ nhật có chu bằng nhau thì diện tích hình tròn là lớn nhất, diện tích hình chữ nhật là bé nhất.

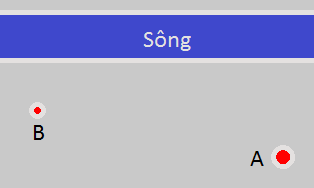
Từ điểm A vuông góc với dòng sông = điểm H
Từ điểm B vuông góc với dòng sông = điểm I
Ta có hình tứ giác ABHI vuông ở H và I.
Vậy để đi nhanh nhất từ nhà đến dòng sông chỉ bằng đường chéo AI. (1 đường chéo luôn ngắn hơn 2 cạnh góc vuông cộng lại)
Để đi nhanh nhất từ dòng sông đến vườn chỉ bằng cạnh góc vuông IB. (con đường ngắn nhất là đường thẳng[góc vuông])
Vậy để chọn con đường gần nhất và nhanh nhất Bác nông dân sẽ đi theo con đường AI và IB. ( để đi nhanh nhất, ngắn nhất và thuận lợi do con đường ko gặp chướng ngại vật[chỉ đến 1 điểm trên dòng sông lấy nước nên giảm chướng ngại vật ở dòng sông])
Lần thứ 2 cũng sẽ đi theo con đường BI và IA.
Từ điểm A vuông góc với dòng sông = điểm H
Từ điểm B vuông góc với dòng sông = điểm I
Ta có hình tứ giác ABHI vuông ở H và I.
Vậy để đi nhanh nhất từ nhà đến dòng sông chỉ bằng đường chéo AI. (1 đường chéo luôn ngắn hơn 2 cạnh góc vuông cộng lại)
Để đi nhanh nhất từ dòng sông đến vườn chỉ bằng cạnh góc vuông IB. (con đường ngắn nhất là đường thẳng[góc vuông])
Vậy để chọn con đường gần nhất và nhanh nhất Bác nông dân sẽ đi theo con đường AI và IB. ( để đi nhanh nhất, ngắn nhất và thuận lợi do con đường ko gặp chướng ngại vật[chỉ đến 1 điểm trên dòng sông lấy nước nên giảm chướng ngại vật ở dòng sông])
Lần thứ 2 cũng sẽ đi theo con đường BI và IA.

a) Tiếng có âm ch hoặc tr:
Đãng trí bác học
Một nhà bác học có tính đãng trí đi tàu hỏa. Khi nhân viên soát vế đến, nhà bác học tìm toát mồ hôi mà chẳng thấy vé đâu. May là người soát vé này nhận ra ông, bèn bảo .
- Thôi, ngài không cần xuất trình vé nữa.
- Nhà bác học vẫn loay hoay tìm vé và nói :
- Nhưng tôi vẫn phải tìm bằng được vé để biết phải xuống ga nào chứ !
b) Tiếng có vần uôt hoặc uôc:
Vị thuốc quý
Nhà thơ Đức nổi tiếng Hai-nơ mắc chứng bệnh mệt mỏi và mất ngủ. Ông dùng rất nhiều thứ thuốc bổ mà vẫn không khỏi. Một bác sĩ đến khám bệnh, bảo ông :
- Mỗi ngày, ngài hãy ăn một quả táo, vừa ăn vừa đi bộ từ nhà đến quảng trường thành phố.
Sau một thời gian ngắn, quả nhiên Hai-nơ khỏi bệnh. Ông ngạc nhiên nói với bác sĩ :
Bây giờ tôi mới biết táo cũng là vị thuốc quý.
Bác sĩ mỉm cười :
- Không phải những quả táo bình thường kia chữa khỏi bệnh cho ngài đâu. Chính những cuộc đi bộ hằng ngày mới là vị thuốc quý, vì chúng bắt buộc ngài phải vận động.

Vì khi bón phân sẽ làm nồng độ các chất tan trong môi trường lớn hơn so với nồng độ chất tan trong các tế bào nên nước trong các tế bào của cây sẽ đi ra ngoài môi trường, khiến cây bị héo.
#CTV49
phương pháp tính ngược từ cuối nha bạn
anh au phai lay 10 qua
vi 3 qua de di vao 3 cong
3 qua de di ra 3 cong
ma 3+3=9 10-9=1