Tim nghiệm của hệ phương trình: x2+xy+y2=1 và x-y-xy=3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trừ vế cho vế phương trình (1) cho (2) ta được:
x 2 + y 2 − y = − 1 ⇔ x 2 + y 2 − y + 1 = 0
Ta có:
x 2 ≥ 0 , ∀ x y 2 − y + 1 = y − 1 2 2 + 3 4 > 0 , ∀ y ⇒ x 2 + y 2 − y + 1 > 0 , ∀ x , y
Do đó phương trình x 2 + y 2 − y + 1 = 0 vô nghiệm
Vậy không tồn tại giá trị của xy
Đáp án cần chọn là: D

Đáp án A
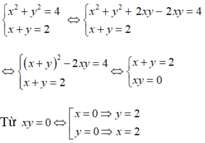
Vậy hệ phương trình có hai nghiệm (x; y) = (0; 2); (x; y) = (2; 0) Từ giả thiết x > y nên x = 2; y = 0 ⇒ xy = 0

Điều kiện: xy > 0
2 x 2 + y 2 + 2 x y = 16 x + y + 2 x y = 16 ⇔ 2 x 2 + y 2 = x + y ⇔ ( x – y ) 2 = 0 ⇔ x = y
Thay x = y vào x + y + x y = 16 ta được
2x + 2|x| = 16 ⇔ x + |x| = 8 ⇒ x = 4 ⇒ y = x = 4
Vậy hệ có một cặp nghiệm duy nhất (x; y) = (4; 4)
Khi đó x y = 4 4 = 1
Đáp án:D

Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

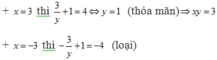

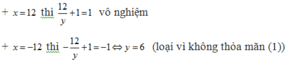
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C

<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
Thân^^
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0

Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C

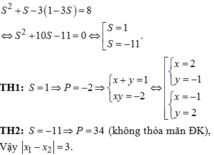
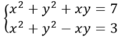
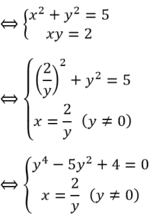


=>(x+y)^2-x+y+3=1
kết hợp với (1) giải ra
kết quả là X=1 và Y=-1