Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
Chứng minh:tam giác ABM = ECM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2016
Hình tự vẽ nha !
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
18 tháng 12 2016
a) Xét ΔABM vàΔECM có:
AM= ME(giả thiết)
AMB=CME( đối đỉnh)
BM=MC( do M là trung điểm của BC)
=> ΔABM= ΔECM( c-g-c).
b) Do ΔABM =ΔECM( theo câu a)
nên BÂM= CÊM ( 2 góc tương ứng).
Mà 2 góc này ở vị trí so le trong nên AB//CE.
10 tháng 12 2018
tham khảo Câu hỏi của huỳnh thị tuyết như - Toán lớp 7 - Học toán với OnlineMath
10 tháng 12 2018
a, Xét tam giác ABM và tam giác ECM có : góc AMB= góc EMC (2 góc đối đỉnh)
MA=ME (gt)
MB =MC (gt)
Nên tam giác ABM = tam giác ECM (c-g-c)
b, Vì tam giác ABM = tam giác ECM (cm câu a) nên góc ABM = góc ECM (2 góc tương ứng )
Mà góc ABM và góc ECM ở vị trí so le trong nên AB // CE
16 tháng 12 2016
Làm tiếp nha:
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành.
=> \(\hept{\begin{cases}AB=CE\left(1\right)\\ABllCE\end{cases}}\)
a ) xét \(\Delta ABM\)và \(\Delta ECM\)có:
\(\hept{\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}}\)
---> \(\Delta ABM=\Delta ECM\left(c.c.c\right)\)
b) Xét \(\Delta ABD\) có BH là đường cao đồng thời đường trung tuyến nên \(\Delta ABD\) cân tại B.
---> BC là phân giác của ABD
\(\Delta ABD\)cân tại B ---> AB = BD (2)
Từ (1),(2) ---> BD = CE
14 tháng 12 2016
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành
\(\Rightarrow\begin{cases}AB=CE\left(1\right)\\AB\backslash\backslash CE\end{cases}\)
a,xét ΔABM và ΔECM có:
\(\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}\)
→ΔABM=ΔECM(c.c.c)
b,Xét ΔABD có BH là đường cao đồng thời là đường trung tuyến
nên ΔABD cân tại B
→BC là phân giác của \(\widehat{ABD}\)
ΔABD cân tại B →AB=BD(2)
Từ (1),(2)→BD=CE
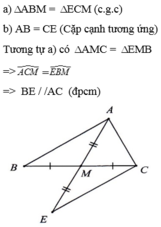
Xét tam giác ABM và tam giác ECM ta có:
MB = MC ( M là trung điểm BC )
góc AMB = góc EMC ( đối đỉnh )
MA = ME ( giả thuyết )
Vậy tam giác ABM = tam giác ECM