Có hai đường dây tải điện cùng một công suất điện với dây dẫn cùng tiết diện, cùng vật liệu. Dây thứ nhất dài 100km, hiệu điện thế hai đầu dây 100000V, dây thứ hai dài 200km, hiệu điện thế là 200000V. Tính tỉ số công suất hao phí của hai dây.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: B
Ta có:
S 1 = S 2 = S ; ρ 1 = ρ 2 = ρ
l 1 = 100 k m , l 2 = 200 k m
U 1 = 100000 k V , U 2 = 200000 k V
+ Điện trở của dây tải: R 1 = ρ l 1 S R 2 = ρ l 2 S
+ Công suất hao phí do tỏa nhiệt trên hai đường dây tải điện là:
P 1 = P 2 R 1 U 1 2 P 2 = P 2 R 2 U 2 2
→ P 1 P 2 = R 1 U 2 2 R 2 U 1 2 = l 1 l 2 U 2 U 1 2
= 100 200 2000000 100000 2 = 2

Chọn B. P 1 = 2 P 2
Do hai dây dẫn cùng làm bằng một chất liệu, cùng một công suất truyền tải và cùng một tiết diện nên ρ, P, S của hai dây bằng nhau.
Công suất hao phí do tỏa nhiệt trên đường dây tải điện khi dùng hiệu điện thế U 1 và U 2 lần lượt là:
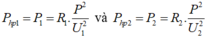
Mặt khác: Điện trở của đường dây tải điện được tính bằng công thức: 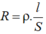
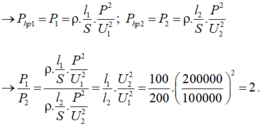
Vậy P 1 = 2 P 2

a, \(\dfrac{R_2}{R_1}=\dfrac{\rho.\dfrac{l_2}{S}}{\rho.\dfrac{l_1}{S}}=\dfrac{\rho.\dfrac{100}{S}}{\rho.\dfrac{25}{S}}=\dfrac{100}{25}=4\) \(\Leftrightarrow R_1=R_2.\dfrac{1}{4}\)
b, \(\dfrac{I_1}{I_2}=\dfrac{\dfrac{U_1}{R_1}}{\dfrac{U_2}{R_2}}=\dfrac{\dfrac{2,5.U_2}{\dfrac{1}{4}.R_2}}{\dfrac{U_2}{R_2}}=\dfrac{2,5}{\dfrac{1}{4}}=10\)

Chọn C.
Công suất hao phí do tỏa nhiệt trên đường dây tải điện khi dùng hiệu điện thế U và U’ lần lượt là:
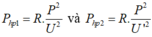
Để giảm hao phí hai lần thì:
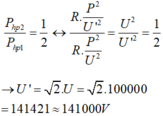

Đáp án: C
Gọi P 1 , U 1 là công suất hao phí và hiệu điện thế ban đầu ( U 1 = 100000 V ) P 2 , U 2 là công suất hao phí và hiệu điện thế cần dùng để giảm hao phí
Ta có: P 1 = P 2 R U 1 2 P 2 = P 2 R U 2 2
Theo đầu bải:
P 2 = P 1 2 → P 2 P 1 = 1 2 = U 1 2 U 2 2 → U 2 = 2 U 1 2 = 2.100000 2 = 141421 V

Ta có: \(P_{hp}=\dfrac{P^2\cdot R}{U^2}\)
Mà \(R=\dfrac{l}{S}\cdot\rho\)
Từ hai công thức trên ta suy ra: \(P_{hp}=\dfrac{P^2\cdot R\cdot\rho}{U^2\cdot S}\)
Nhìn vào công thức nếu giảm \(S\) 2 lần và tăng \(U\) 2 lần thì \(P_{hp}\) giảm 2 lần do \(P_{hp}\) tỉ lệ nghịch với \(U^2,S\)
\(\dfrac{R_1}{R_2}=\dfrac{1}{2}\) và \(\dfrac{U_1}{U_2}=\dfrac{1}{2}\)
Tỉ số công suất hao phí của hai dây:
\(\dfrac{P_{hp1}}{P_{hp2}}=\dfrac{\dfrac{P^2.R_1}{U^2_1}}{\dfrac{P^2.R_2}{U^2_2}}=\dfrac{\dfrac{R_1}{U^2_1}}{\dfrac{R_2}{U^2_2}}=\dfrac{R_1.U^2_2}{R_2.U_1^2}=\dfrac{1}{2}.\left(\dfrac{2}{1}\right)^2=2\)
=> Php1 = 2.Php2
\({\wp _{h{p_1}}} = {{R{\wp ^2}} \over {U_1^2}} = {{{{\rho {l_1}{\wp ^2}} \over S}} \over {U_1^2}} = {{{{100\rho {\wp ^2}} \over S}} \over {{{100000}^2}}}\,\,\,\,\,\,\\ {\wp _{h{p_2}}} = {{R{\wp ^2}} \over {U_2^2}} = {{{{\rho {l_2}{\wp ^2}} \over S}} \over {U_2^2}} = {{{{200\rho {\wp ^2}} \over S}} \over {{{200000}^2}}}\,\,\,\,\,\,\\ \Rightarrow \dfrac{{\wp _{h{p_1}}} }{{\wp _{h{p_2}}} }=2\)