Cho x+3y>=1 . Giá trị nhỏ nhất của biểu thức là A=x^2+y^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng bđt Cô-si \(1=x^2+y^2\ge2xy\)
\(\Rightarrow xy\le\frac{1}{2}\)
Ta có \(A=\frac{-2xy}{1+xy}\ge\frac{-\frac{2.1}{2}}{1+\frac{1}{2}}=-\frac{2}{3}\)
\("="\Leftrightarrow x=y=\frac{1}{\sqrt{2}}\)

a) \(\left(\frac{x+3}{x-2}+\frac{x+2}{3-x}+\frac{x+2}{x^2-5x+6}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{x+3}{x-2}-\frac{x+2}{x-3}+\frac{x+2}{x^2-2x-3x+6}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\frac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}\right).\frac{x+1}{1-x}\)
=\(\frac{-3+x}{\left(x-2\right)\left(x-3\right)}.\frac{x+1}{1-x}\)
=\(\frac{1}{\left(x-2\right)}.\frac{x+1}{1-x}\)
=\(\frac{x+1}{\left(x-2\right)\left(1-x\right)}\)
b) Để A >1 \(\Leftrightarrow\frac{x+1}{\left(x-2\right)\left(1-x\right)}>1\)
\(\Leftrightarrow\frac{-\left(1-x\right)\left(3-x\right)}{\left(x-2\right)\left(1-x\right)}\)
\(\Leftrightarrow\frac{x-3}{x-2}>0\)
\(\Rightarrow\orbr{\begin{cases}x-3\ge0\\x-2>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge3\\x>2\end{cases}\Leftrightarrow}x\ge3}\)
\(\Rightarrow\orbr{\begin{cases}x-3< 0\\x-2< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 2\end{cases}\Leftrightarrow}x< 2}\)
Vậy ...


đúng đấy mình có 1 bài như thế cô mình bảo kêt quả là 1/5

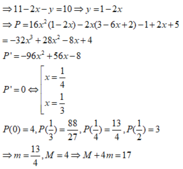
GTNN bằng 5,5 khi y=-3/4
Min =5,5 ..check mk nhá