Nếu tam giác ABC có góc BAC = 500 và AB = AC thì số đo của góc ABC bằng:
A.650 B. 750 C. 550 D. 450
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2023
Xét `\Delta ABC`:
$\widehat {A}+ \widehat {B} + \widehat {C}=180^0 (\text {định lý tổng số đo 3 góc trong 1 tam giác})$
`->` $ 50^0+ 65^0+ \widehat {C}=180^0$
`->` $\widehat {C} = 180^0-50^0-65^0=65^0$
Xét các đáp án trên `-> B.`
CM
18 tháng 1 2017
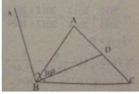
Tia BD nằm giữa hai tia BA và BC nên
∠ABC = ∠ADB + ∠DBC ; ∠DBC =∠ABC - ∠ADB
∠DBC = 55 0 - 30 0 = 25 0
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có∠ABx = ∠DBx - ∠DBA= 90 0 - 30 0 = 60 0
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có ∠ABx = ∠DBx + ∠DBA= 90 0 + 30 0 = 120 0
Answer:
A C B 50 độ
Ta xét tam giác ABC
AB = AC (gt)
=> Tam giác ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Ta có: \(\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180^o\)
Mà \(\widehat{ABC}=\widehat{ACB}\) (chứng minh trên)
\(\Rightarrow\widehat{BAC}+2\widehat{ABC}=180^o\)
\(\Rightarrow2\widehat{ABC}=180^o-\widehat{BAC}\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-50^o}{2}=\frac{130^o}{2}=65^o\)