5x3-9x2=2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lời giải:
Khi $m=-3$ thì $f(x)=5x^3-9x^2+2x-3$
$f(x)=5x^3-9x^2+2x-3=5x^2(x-1)-4x(x-1)-2(x-1)-5$
$=(x-1)(5x^2-4x-2)-5$
Như vậy, với mọi số tự nhiên $x\neq 1$, để $f(x)\vdots x-1$ thì $5\vdots x-1$ hay $x-1$ là ước của $5$
$\Rightarrow x-1\in\left\{\pm 1;\pm 5\right\}$
$\Leftrightarrow x\in\left\{2;0;-4;6\right\}$
Mà $x$ tự nhiên nên $x\in\left\{0;2;6\right\}$
9 tháng 9 2021
a)\(f\left(x\right)=5x^3-9x^2+2x+m=5x^2\left(x+2\right)-19x\left(x+2\right)+40\left(x+2\right)-80+m=\left(x+2\right)\left(5x^2-19x+40\right)+m-80\)
Để \(f\left(x\right)⋮g\left(x\right)\) thì \(m-80=0\Leftrightarrow m=80\)
b) \(f\left(x\right)=\left(x+2\right)\left(5x^2-19x+40\right)+m-80\)
Để f(x) chia g(x) có số dư bằng 3 thì \(m-80=3\Leftrightarrow m=83\)
9 tháng 1
`#3107.101107`
`A(x) = 3x - 9x^2 + 4x + 5x^3 + 7x^2 + 1`
`= (3x + 4x) - (9x^2 - 7x^2) + 5x^3 + 1`
`= 7x - 2x^2 + 5x^3 + 1`
`B(x) = 5x^3 - 3x^2 + 7x + 10`
`A(x) - B(x) = 7x - 2x^2 + 5x^3 + 1 - (5x^3 - 3x^2 + 7x + 10)`
`= 7x - 2x^2 + 5x^3 + 1 - 5x^3 + 3x^2 - 7x - 10`
`= (7x - 7x) + (3x^2 - 2x^2) + (5x^3 - 5x^3) - (10 - 1)`
`= x^2 - 9`
`=> C(x) = x^2 - 9`
`C(x) = 0`
`=> x^2 - 9 = 0`
`=> x^2 = 9 => x^2 = (+-3)^2 => x = +-3`
Vậy, nghiệm của đa thức `C(x)` là `x \in {3; -3}.`
27 tháng 4 2023
`5x^3-9x^2-3-6`
`= 5x^3-9x^2-9`
Sắp xếp: `-9-9x^2+5x^3`
TT
1
CV
0
CM
19 tháng 6 2018
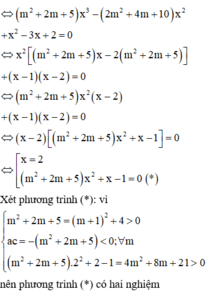
Vì f(x) là hàm đồng biến nên mỗi phương trình (1);(2);(3) đều chỉ có 1 nghiệm duy nhất và ba nghiệm của phương trình này khác nhau.
Từ đó phương trình g f x = 0 có ba nghiệm phân biệt.
Chọn: C
\(5x^3-9x^2=2x\)
\(\Leftrightarrow x\left(5x^2-9x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-\dfrac{1}{5}\end{matrix}\right.\)