4 số nguyên khác nhau lập thành 1 cấp số cộng. 1 trong 4 số này bằng tổng bình phương của 3 số còn lại. Xác định các số đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 1 2021
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
2 tháng 1 2021
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
CM
14 tháng 12 2018
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Ta có:
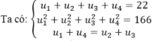
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+ 103=1408
Đáp án là D
CM
6 tháng 3 2017
Đáp án là D
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4 và công sai là d
Ta có: u2 = u1 + d; u3= u1 + 2d; u4 = u1 + 3d
Theo giả thiết ta có:
u
1
+
u
2
+
u
3
+
u
4
=
22
u
1
2
+
u
2
2
+
u
3
2
+
u
4
2
=
166
⇔
u
1
+
u
1
+
d
+
u
1
+
2
d
+
u
1
+
3
d
=
22
u
1
2
+
(
u
1
+
d
)
2
+
(
u
1
+
2
d
)
2
+
(
u
1
+
3
d
)
2
=
166
⇔
4
u
1
+
6
d
=
22
4
u
1
2
+
12
u
1
d
+
14
d
2
=
166
⇒
2
u
1
+
3
d
=
11
(
1
)
2
u
1
2
+
6
u
1
d
+
7
d
2
=
83
(
2
)
Từ (1) suy ra: u 1 = 11 − 3 d 2 thế vào (2) ta được:
2. 11 − 3 d 2 2 + 6. 11 − 3 d 2 . d + 7 d 2 = 83 ⇔ d = 3 ⇒ u 1 = 1 d = − 3 ⇒ u 1 = 10
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng:
1 3 + 4 3 + 7 3 + 10 3 = 1408
16 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
long long a,b,c;
bool kt;
int main()
{
cin>>a>>b>>c;
kt=false;
if (a==(b+c)/2) kt=true;
if (b==(a+c)/2) kt=true;
if (c==(b+a)/2) kt=true;
if (kt==false) cout<<"Khong lap duoc";
else cout<<"Lap duoc";
return 0;
}
CM
3 tháng 10 2018
Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
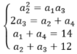
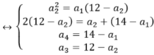
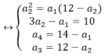
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
TD
0
3 tháng 6 2016
a^2 + b^2 + c^2 + d^2 = e^2
a^2 + b^2 + c^2 + e^2 = d^2
a^2 + b^2 + d^2 + e^2 = c^2
a^2 + d^2 + e^2 + c^2 = b^2
d^2 + e^2 + c^2 + b^2 = a^2
=> 4( a^2 + b^2 + c^2 + d^2 + e^2 ) = a^2 + b^2 + c^2 + d^2 + e^2
=> 3( a^2 + b^2 + c^2 + d^2 + e^2 ) = 0
=> a^2 + b^2 + c^2 + d^2 + e^2 = 0
=> a = b = c = d = e = 0
6 tháng 6 2016
a^2 + b^2 + c^2 + d^2 = e^2
a^2 + b^2 + c^2 + e^2 = d^2
a^2 + b^2 + d^2 + e^2 = c^2
a^2 + d^2 + e^2 + c^2 = b^2
d^2 + e^2 + c^2 + b^2 = a^2
=> 4( a^2 + b^2 + c^2 + d^2 + e^2 ) = a^2 + b^2 + c^2 + d^2 + e^2
=> 3( a^2 + b^2 + c^2 + d^2 + e^2 ) = 0
=> a^2 + b^2 + c^2 + d^2 + e^2 = 0
=> a = b = c = d = e = 0
Gọi 4 số nguyên là \(a_1< a_2< a_3< a_4\) \(\Rightarrow\left\{{}\begin{matrix}a_2=a_1+d\\a_3=a_1+2d\\a_4=a_1+3d\end{matrix}\right.\) với \(d\in Z^+\)
\(a_4=a_1^2+a_2^2+a_3^2\)
\(\Leftrightarrow a_1+3d=a_1^2+\left(a_1+d\right)^2+\left(a_1+2d\right)^2\)
\(\Leftrightarrow a_1+3d=3a_1^2+6a_1d+5d^2\)
\(\Leftrightarrow3a_1^2+\left(6d-1\right)a_1+5d^2-3d=0\)
\(\Delta=\left(6d-1\right)^2-12\left(5d^2-3d\right)\ge0\)
\(\Leftrightarrow-24d^2+24d+1\ge0\Rightarrow\dfrac{6-\sqrt{42}}{12}\le d\le\dfrac{6+\sqrt{42}}{12}\)
\(\Rightarrow\left[{}\begin{matrix}d=0\left(ktm\right)\\d=1\end{matrix}\right.\) \(\Rightarrow3a_1^2+5a_1+2=0\Rightarrow\left[{}\begin{matrix}a_1=-1\\a_1=-\dfrac{2}{3}\left(ktm\right)\end{matrix}\right.\)
Vậy 4 số đó là -1; 0; 1; 2