Cho mặt phẳng Oxy, cho tam giác ABC với A(3;1), B(-1;-1), C(6;0)
a. Tính tọa độ trung điểm I của đoạn AB và trọng tâm G của tam giác ABC
b. Tính chu vi tam giác ABC và Cos A
c. Tìm tọa độ trực tâm H của tam giác ABC
* Giúp mình với ạ, mình đang cần gấp ạ *
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2023
\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)
\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)
\(BC=\left(-3;4\right)\Rightarrow BC=5\)
Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2023
\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)
\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)
\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)
Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)
HV
1
6 tháng 1 2023
\(AB=\sqrt{\left(0+1\right)^2+\left(2+3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left(2+1\right)^2+\left(1+3\right)^2}=\sqrt{3^2+4^2}=5\)
\(BC=\sqrt{\left(2-0\right)^2+\left(1-2\right)^2}=\sqrt{5}\)
=>\(C=\sqrt{26}+5+\sqrt{5}\left(cm\right)\)
30 tháng 3 2023
\(AB=\sqrt{\left(5-1\right)^2+\left(-3+1\right)^2}=2\sqrt{5}\)
\(AC=\sqrt{\left(0-1\right)^2+\left(1+1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(0-5\right)^2+\left(1+3\right)^2}=\sqrt{29}\)
=>C=3 căn 5+căn 29
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;-2\right)\\\overrightarrow{AC}=\left(4;-2\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=-1.4+\left(-2\right).\left(-2\right)=0\)
\(\Rightarrow\Delta ABC\) vuông tại A
25 tháng 3 2023
Gọi (C): x^2+y^2-2ax-2by+c=0 là PT đường tròn ngoại tiêpΔACB
Theo đề, ta có:
2^2+(-1)^2-4a+2b+c=0 và 1+4+2a-4b+c=0 và 16+1+8a+2b+c=0
=>-4a+2b+c=-5 và 2a-4b+c=-5 và 8a+2b+c=-17
=>a=-1; b=-1; c=-7
=>x^2+y^2+2x+2y-7=0
=>x^2+2x+1+y^2+2y+1=9
=>(x+1)^2+(y+1)^2=9
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 5 2021
\(\overrightarrow{BC}=\left(-4;-4\right)=-4\left(1;1\right)\)
Phương trình BC: \(1\left(x-4\right)-1\left(y-1\right)=0\Leftrightarrow x-y-3=0\)
Phương trình AH qua A và vuông góc BC:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
H là giao điểm AH và BC nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}x-y-3=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow H\left(3;0\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(2;-2\right)\Rightarrow AH=2\sqrt{2}\)
CM
26 tháng 10 2019
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)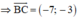 
Phương trình đường cao AH đi qua A(2;-1) nhận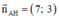 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.