Cho tam giác ABC, M là điểm nằm trên tia phân giác góc ngoài đỉnh C. CMR: MA+MB>AC+BC
Help me every body!!!!!!!!!!!!!! E đang cần gấp lắm ạ !!!!!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
HV
2
1 tháng 5 2018
Hình thì chắc bạn tự vẽ nha!!!
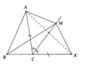
Từ A vẽ AH vuông góc với tia phân giác Cy của góc ACx, cắt tia BC tại D. Ta có tam giác MAH= tam giác MDH(c.g.c), suy ra MA=MD. Tam giác MBD có MD+MB>BD nên MA+MB>BD. Mà BD=CD+BC=AC+BC
Vậy MA+MB>AC+BC(đpcm)
Chúc bạn học giỏi!!! Nhớ k cho mình đó!!!Cảm ơn bạn nhiều!!!
:#
NM
0
PT
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB
1
CM
31 tháng 8 2017
Trên tia đối của tia CB lấy điểm A' sao cho CA' = CA. Sử dụng tính chất của tam giác cân ta có được CM là đường trung trực của AA' Þ MA = MA'. Sử dụng bất đẳng thức trong tam giác A'MB ta có: CA + CB = CA' + CB = BA' <MA' + MB Þ CA + CB < MA + MB.
CM
21 tháng 5 2019
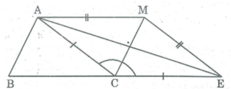
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME (tính chất đường trung trực)
Ta có: AC + BC = CE + BC = BE (1)
MA + MB = ME + MB (2)
Trong ∆ MBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.
cái này người ta thường gọi là "đã ngu còn tỏ ra nguy hiểm". Tiếng anh đã ngu rồi lại cứ thích nói tiếng anh
Tốt gỗ hơn tốt nước sơn