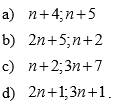Tìm số tự nhiên p để các số sau là số nguyên tố p + 2; p + 6;p + 8; p + 12 và p+14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau

a) gs cả 2 số đều lẻ thì tổng chẵn
mà 2 số nguyên tố lẻ nên >2 => tổng >2 mà tổng chẵn => ko là sô nguyên tố => trái đề bài
suy ra 1 trong 2 số là số chẵn mà 2 số là số nguyên tố => một số =2
mà 2 số này là 2 số nguyên tố liên tiếp nên số còn lại là 3
b) đặt 19n=p ( p nguyên tố);
vì p nguyên tố nên phân tích p thành tích 2 số tự nhiên ta có p=p*1
=> p=19;n=1
c)đặt (p+1)(p+7)=a ( a nguyên tố)
vì a nguyên tố nên phân tích a thành tích 2 số tự nhiên ta có a=a*1; mà p+1<p+7
nên p+1=1 và p+7=a => p=0;a=7

a) Do 97 là số nguyên tố mà 97.a cũng là số nguyên tố nên a=1
b) 101 là số nguyên tố để 101.b là hợp số thì b>=2
c) Xét p=2 thì p2+974 là hợp số (loại)
Xét p=3 thì p2+974 là số nguyên tố
Xét p=3k+1 và 3k+2 thì p2+974 là hợp số (loại)
Vậy p=3 thì p2+974 là số nguyên tố

Với \(x=0\Rightarrow n^5+n^4+1=1\left(loai\right)\)
Với \(x=1\Rightarrow n^5+n^4+1=3\left(TM\right)\)
Với \(x\ge2\) ta có:
\(n^5+n^4+1\)
\(=n^5-n^2+n^4-n+n^2+n+1\)
\(=n^2\left(n^3-1\right)+n\left(n^3-1\right)+\left(n^2+n+1\right)\)
\(=n^2\left(n-1\right)\left(n^2+n+1\right)+n\left(n-1\right)\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=A\cdot\left(n^2+n+1\right)+B\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=\left(n^2+n+1\right)\left(A+B+1\right)\) là hợp số với mọi \(n\ge2\)
Vậy \(n=1\)
Với \(n=0\Rightarrow A=n^8+n+1=1\left(KTM\right)\) vì 1 không là SNT
Với \(n=1\Rightarrow A=n^8+n+1=3\left(TM\right)\) vì 3 là SNT
Với \(n\ge2\) ta có:
\(A=n^8+n+1\)
\(=\left(n^8-n^2\right)+n^2+n+1\)
\(=n^2\left(n^6-1\right)+\left(n^2+n+1\right)\)
\(=n^2\left[\left(n^3\right)^2-1^2\right]+\left(n^2+n+1\right)\)
\(=n^2\left(n^3-1\right)\left(n^3+1\right)+\left(n^2+n+1\right)\)
\(=X\cdot\left(n^3-1\right)+\left(n^2+n+1\right)\)
\(=X\left(n-1\right)\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=X'\left(x^2+n+1\right)+\left(n^2+n+1\right)\)
\(=\left(n^2+n+1\right)\left(X'+1\right)\) là hợp số với \(n\ge2\)
Vậy \(n=1\)

a) Do 97 là số nguyên tố mà 97.a cũng là số nguyên tố nên a=1
b) 101 là số nguyên tố để 101.b là hợp số thì b>=2
c) Xét p=2 thì p2+974 là hợp số (loại)
Xét p=3 thì p2+974 là số nguyên tố
Xét p=3k+1 và 3k+2 thì p2+974 là hợp số (loại)
Vậy p=3 thì p2+974 là số nguyên tố