Tìm x, y biết: 6x2+6y2+10xy+2x-2y+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2021
\(a,=18x^4-24x^3+30x\\ b,=3x^2y+6xy^2+x^2-6xy^2-12y^3-2xy=3x^2y+x^2-12y^3-2xy\\ c,=-3x^2+4xy-2x\\ d,=\left(x-y\right)^2\left[4\left(x-y\right)^3+2\left(x-y\right)-3\right]:\left(x-y\right)^2\\ =4\left(x-y\right)^3+2\left(x-y\right)-3\)
26 tháng 10 2021
a: \(=18x^4-24x^3+30x^2\)
b: \(=3x^2y+6xy^2+x^2-6xy^2-12y^3-2xy\)
\(=x^2-12y^3+3x^2y-2xy\)
28 tháng 10 2021
Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)
NY
2
3 tháng 7 2019
\(2x^2+10xy+14y^2+2x+2y+2=0\)
\(\Leftrightarrow\left(x^2+4y^2+1+2x+4xy+4y\right)+\left(x^2+6xy+9y^2\right)+\left(y^2-2y+1\right)=0\)
\(\Leftrightarrow\left(x+2y+1\right)^2+\left(x+3y\right)^2+\left(y-1\right)^2=0\)
Vì \(\hept{\begin{cases}\left(x+2y+1\right)^2\ge0;\forall x,y\\\left(x+3y\right)^2\ge0;\forall x,y\\\left(y-1\right)^2\ge0;\forall x,y\end{cases}}\)
\(\Rightarrow\left(x+2y+1\right)^2+\left(x+3y\right)^2+\left(y-1\right)^2\ge0;\forall x,y\)
Do đó :\(\left(x+2y+1\right)^2+\left(x+3y\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+2y+1\right)^2=0\\\left(x+3y\right)^2=0\\\left(y-1\right)^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1\\x=-3\\y=1\end{cases}}\)
Vậy x=-3 và y=1
Kiến thức bổ sung
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
3 tháng 7 2019
\(\Leftrightarrow4x^2+20xy+28y^2+4x+4y+4=0\)
\(\Leftrightarrow\left(4x^2+4x+20xy+25y^2+10y+1\right)+\left(3y^2-6y+3\right)=0\)
\(\Leftrightarrow\left(2x+5y+1\right)^2+3\left(y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}2x+5y+1=0\\y-1=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-3\\y=1\end{cases}}\)
N
0
NK
0
8 tháng 8 2015
a) <M = -4x^2 + 6xy - y^2 - (5x^2 - 2xy)
= -4x^2 + 6xy - y^2 - 5x^2 + 2xy
= -9x^2 +8xy - y^2
b) M = (24xy^2 - 13x^2y -+2x^3 ) - (10xy^2 + 2x^2 + 3 )
= 24xy^2 - 13x^2y + 2x^3 - 10xy^2 - 2x^2 - 3
= 14xy^2 - 13x^2y + 2x^3 - 2x^2-3
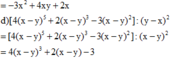
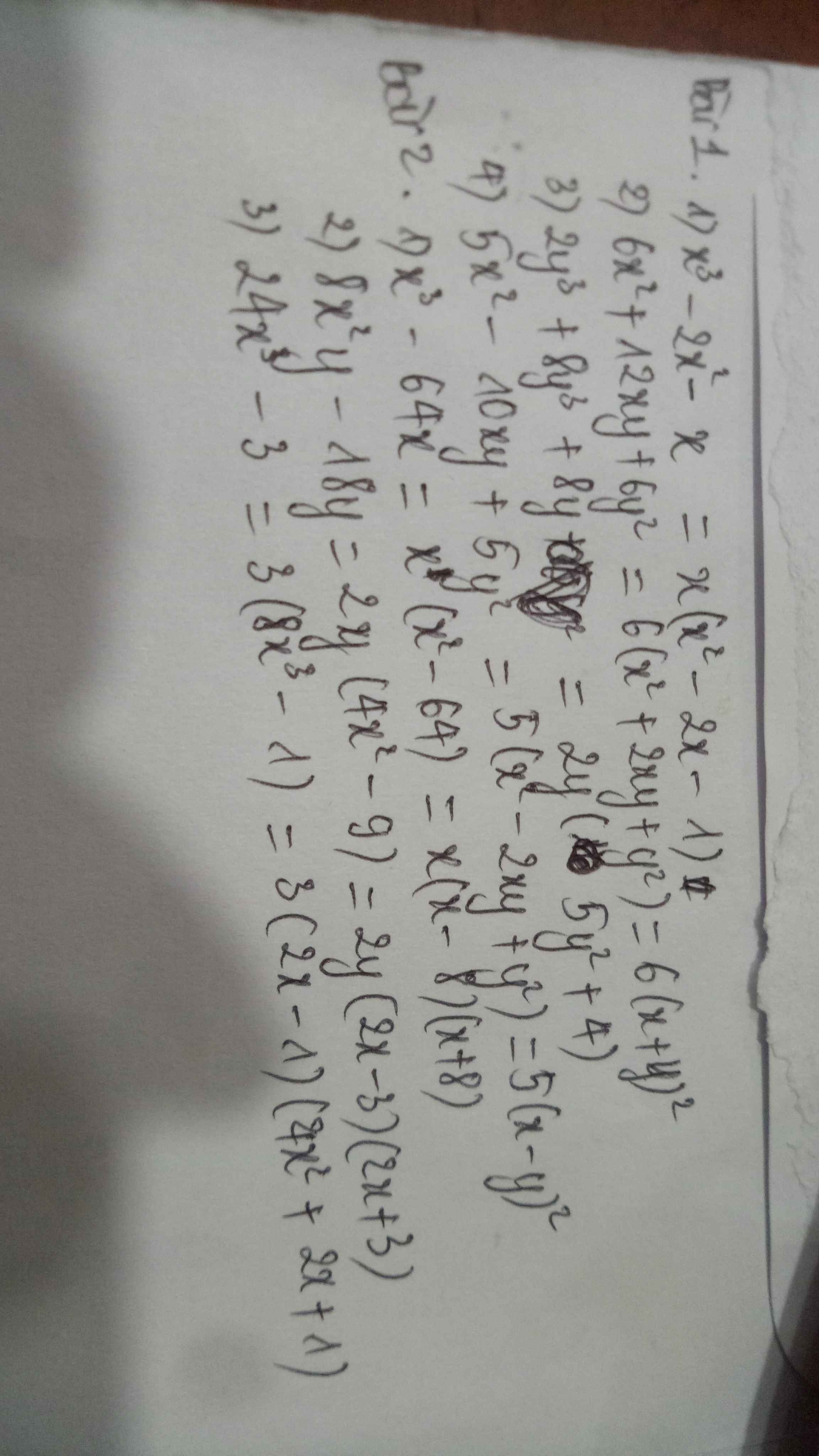
\(6x^2+6y^2+10xy+2x-2y+2=0\)
\(\Leftrightarrow5x^2+10xy+5y^2+x^2+2x+1+y^2-2y+1=0\)
\(\Leftrightarrow5\left(x+y\right)^2+\left(x+1\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+1=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=1\end{cases}}\).