vời x là số nguyên, giá trị nhỏ nhất của biểu thức A = (x2-5)2 là ....
giải thích đầy đủ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
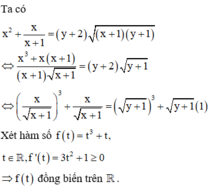
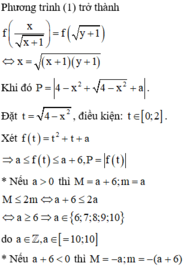
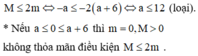
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3

Bài 1:
\(A=x^2+6x+9+x^2-10x+25\)
\(=2x^2+4x+34\)
\(=2\left(x^2+2x+17\right)\)
\(=2\left(x+1\right)^2+32>=32\forall x\)
Dấu '=' xảy ra khi x=-1

Áp dụng BĐT trị tuyệt đối:
\(M=\left|x-2019\right|+\left|2021-x\right|+2020\left|x-2020\right|\)
\(M\ge\left|x-2019+2021-x\right|+2020\left|x-2020\right|=2+2020\left|x-2020\right|\ge2\)
\(\Rightarrow M_{min}=2\) khi \(\left\{{}\begin{matrix}\left(x-2019\right)\left(2021-x\right)\ge0\\\left|x-2020\right|=0\end{matrix}\right.\) \(\Rightarrow x=2020\)

Chọn B.
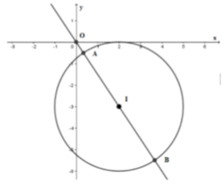
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
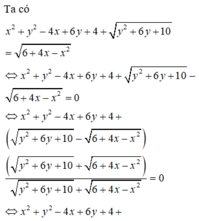
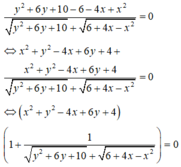


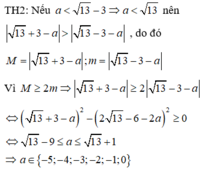


a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.
thông điệp nhỏ:
hay khi ko muốn k
ai tích mình tích lại
Là 1 đảm bảo luôn nhé
Ai tích mk mk tích lại cho