một cano xuôi dòng từ bến a đến bến b mất 2 giờ 30 phút và ngược dòng từ bến B về bến A mất 3 giờ. Tính khoảng cách giữa 2 bến. biết vận tốc của dòng nước là 6km/h
help meh pls;-;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2022
Gọi khoảng cách từ A đến B là x ( km ) ( x>0 )
Vận tốc xuôi dòng là: \(\dfrac{x}{4}\) (h)
Vận tốc ngược dòng là: \(\dfrac{x}{5}\) (h)
Theo đề bài ta có pt:
\(\dfrac{x}{4}-\dfrac{x}{5}=2.2\)
\(\Leftrightarrow\dfrac{5x-4x}{20}=\dfrac{80}{20}\)
\(\Leftrightarrow x=80\left(tm\right)\)
Vậy khoảng cách từ A đến B là 80km
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
Gọi vận tốc cano khi nước lặng là x km/h với x>2
Vận tốc cano khi xuôi dòng: x+2 (km/h)
Quãng đường cano đi xuôi dòng: \(4\left(x+2\right)\)
Vận tốc cano khi ngược dòng: \(x-2\) (km/h)
Quãng đường cano đi ngược dòng: \(5\left(x-2\right)\) (km/h)
Do độ dài quãng đường xuôi dòng và ngược dòng như nhau nên ta có pt:
\(4\left(x+2\right)=5\left(x-2\right)\)
\(\Leftrightarrow x=18\) (km/h)
Độ dài AB: \(4\left(18+2\right)=80\left(km\right)\)
NH
28 tháng 3 2020
Gọi vận tốc thực cano là x (km/h, x > 4)
Vận tốc xuôi dòng của cano là: x + 4 (km/h)
Quãng đường cano xuôi dòng từ bến A đến bến B là: 3(x + 4) (km)
Vận tốc ngược dòng của cano là: x - 4 (km/h)
Quãng đường cano ngược dòng từ bến B đến bến A là: 5(x - 4) (km)
Theo bài ra, ta có phương trình: 3(x + 4) = 5(x - 4)
<=> 3x + 12 = 5x - 20
<=> 3x - 5x = -20 - 12
<=> -2x = -32
<=> x = 16 (thỏa mãn)
Vận tốc xuôi dòng từ A đến B của cano là: 16 + 4 = 20 (km/h)
Vậy Khoảng cách giữa bến A và bến B là: 20 . 3 = 60 (km)
28 tháng 3 2020
Gọi: - Vận tốc thực của cano là Vt
- Vận tốc cano đi xuôi dòng là (Vt+4)
- Vận tốc cano đi ngược dòng là (Vt-4)
Ta có :
Khi cano đi xuôi dòng : S=3(Vt+4) (*)
Khi cano đi ngược dòng : S=5(Vt-4) (**)
Từ (*) và (**) , ta có: 3(Vt+4) = 5(Vt-4)
=> 3Vt + 12 = 5Vt - 20
=> 3Vt - 5Vt = -12-20
=> -2Vt = -32
=> Vt = 16 (km/h)
Khoảng cách giữa hai bến AB là:
S = 3(Vt+4)
=> S = 3(16 +4)
=> S = 60 (km)
CM
23 tháng 6 2019
Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
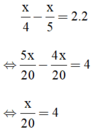
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)
H9
HT.Phong (9A5)
CTVHS
27 tháng 3 2023
Gọi z là quãng đường khoảng cách giữa A và B (x>0)
Khi đó vận tốc lượt đi \(\dfrac{x}{\dfrac{1}{2}}\left(km/\right)h\)
Và vận tốc lượt về: \(\dfrac{x}{\dfrac{3}{5}}\left(km/h\right)\)
Vận tốc lúc đi lớn hơn vận tốc lúc về là: \(2.2=4\left(km/h\right)\)
Vậy ta có phương trình:
\(\dfrac{x}{\dfrac{1}{2}}-\dfrac{x}{\dfrac{3}{5}}=4\)
\(\Leftrightarrow\dfrac{\dfrac{3}{5}x}{\dfrac{3}{10}}-\dfrac{\dfrac{1}{2}x}{\dfrac{3}{10}}=\dfrac{\dfrac{6}{5}}{\dfrac{3}{10}}\)
\(\Leftrightarrow\dfrac{3}{5}x-\dfrac{1}{2}x=\dfrac{6}{5}\)
\(\Leftrightarrow\dfrac{1}{10}x=\dfrac{6}{5}\)
\(\Leftrightarrow x=\dfrac{\dfrac{6}{5}}{\dfrac{1}{10}}=12\left(km\right)\left(tmđk\right)\)
Vậy quãng đường AB dài 12 km
NK
14 tháng 5 2023
Gọi vận tốc của thuyền là v ta có:
Khi xuôi dòng : \(v+2\)
Khi ngược dòng: \(v-2\)
Do quãng đường không đổi nên ta có phương trình:
\(6.\left(v+2\right)=7.\left(v-2\right)\Leftrightarrow6v+12=7v-14\Leftrightarrow v=26\)(km/h)
\(\Rightarrow S=v_{ngược}\times t_{ngược}=\left(v-v_{nước}\right)\times t_{ngược}=\left(26-2\right)\times7=168\left(km\right)\)
Vậy quãng đường AB dài 168 km
28 tháng 1 2018
| V(km/h) | t(h) | S(km) | |
| Ca nô xuôi dòng | x4 | 4 | x |
| Ca nô ngược dòng | x5 | 5 | x |
Giải:
Gọi khoảng cách giữa hai bến ca nô là x km(x>0)
Vậy: Vận tốc xuôi dòng của ca nô là x4 (km/h)
Vận tốc ngược dòng của ca nô là x5 (km/h)
Mà vận tốc của dòng nước là 2km/h Nên khi xuôi dòng vận tốc của ca nô nhiều hơn vận tốc khi đi ngược dòng của ca nô là 4km/h
Do đó ta có phương trình: x4−x5=4
⇔5x−4x=4.20⇔x=80(TMĐK)
Vậy khoảng cách giữa hai điểm A và B là 80km
13 tháng 7 2016
Gọi quãng đường AB là l
vận tốc của ca nô là : \(V_c\)
vận tốc của dòng nước là: \(V_n\)
*) Khi ca nô đi xuôi dòng từ A-> B thì \(l=4\left(V_c+V_n\right)\)
*) Khi ca nô đi ngược dòng từ A -> B thì \(l=5\left(V_c-V_n\right)\)
=> \(4\left(V_c+V_n\right)=5\left(V_c-V_n\right)=>4V_c+4V_n=5V_c-5V_n=>9V_n=V_c=>V_c=180km\)/h
=>l=5.160=800km.
Gọi vận tốc thực của cano là \(x\left(km/h\right),x>6\).
Vận tốc của cano khi đi xuôi dòng là: \(x+6\left(km/h\right)\).
Vận tốc của cano khi đi ngược dòng là: \(x-6\left(km/h\right)\).
Ta có phương trình:
\(2,5\left(x+6\right)=3\left(x-6\right)\)
\(\Leftrightarrow x=66\left(km/h\right)\)
Khoảng cách giữa hai bến là: \(3\left(66-6\right)=180\left(km\right)\).
Trả lời:
Đổi: 2 giờ 30 phút = 2,5 giờ
Gọi x là vận tốc thực của cano ( km/h; x > 6 )
=> Vân tốc của cano khi xuôi dòng từ A -> B là: x + 6 (km/h)
Quãng đường cano đi từ A -> B là: 2,5 ( x + 6 ) (km)
Vận tốc của cano khi đi ngược dòng từ B -> A là: x - 6 (km/h)
Quãng đường cano đi từ B -> A là: 3 ( x - 6 ) (km)
Vì quãng đường cano đi được lúc xuôi dòng và ngược dòng là như nhau
nên ta có phương trình:
2,5 ( x + 6 ) = 3 ( x - 6 )
<=> 2,5x + 15 = 3x - 18
<=> 2,5x - 3x = -18 - 15
<=> -0,5x = -33
<=> x = 66 (tm)
Vậy khoảng cách 2 bến A, B là : 3 ( 66 - 6 ) = 3 . 60 = 180 (km)