cho tam giác ABC đều có cạnh Bằng 5cm Đường cao là AH . tính AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(BH=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
a: Đề sai rồi bạn
a.=> BC = BH + CH = 1 + 3 = 4 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=HB^2+AH^2\)
\(AB=\sqrt{1^2+2^2}=\sqrt{5}cm\)
áp dụng định lí pitago vào tam giác vuông AHC
\(AC^2=AH^2+HC^2\)
\(AC=\sqrt{2^2+3^2}=\sqrt{13}cm\)

a, Theo định lí Pytago tam giác ABH vuông tại H
\(AB=\sqrt{BH^2+AH^2}=\sqrt{5}cm\)
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4+9}=\sqrt{13}\)cm
-> BC = HB + HC = 4 cm
b, Ta có tam giacs ABC đều mà BH là đường cao hay BH đồng thời là đường trung tuyến
=> AH = AC/2 = 5/2
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=\dfrac{5\sqrt{3}}{2}cm\)

Do `\Delta ABC` đều
`-> AB=AC=BC`
`-> AB = 2BH`
Xét `\Delta ABH` vuông tại `H` `( AH` là đường cao `)`
ta có `:` `AB^2 = BH^2 + AH^2`
`=> 4BH^2 = BH^2 + AH^2`
`=> 3BH^2 = AH^2`
`=> BH = ( AH )/( \sqrt{3} )`
`=> a = AB = ( AH )/( \sqrt{3} )`
Vậy `...`

Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=1.8cm\\CH=3.2cm\\AH=2.4cm\end{matrix}\right.\)
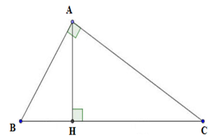
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

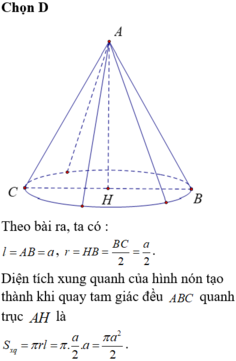
Bán kính đáy:

Diện tích xung quanh của hình nón đó là:
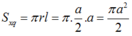
Chọn: D

ΔABC đều có AH là đường cao
nên \(AH=\dfrac{AB\cdot\sqrt{3}}{2}=\dfrac{2a\cdot\sqrt{3}}{2}=a\sqrt{3}\)
=>\(\left|\overrightarrow{AH}\right|=AH=a\sqrt{3}\)
Xét tam giác ABC đều có đường cao AH ta có:
\(\Rightarrow BH=HC=\dfrac{BC}{2}=\dfrac{2a}{2}=a\)
Mà: \(AH=\sqrt{AB^2-BH^2}=\sqrt{\left(2a\right)^2-a^2}\)
\(\Rightarrow AH=\sqrt{4a^2-a^2}=a\sqrt{3}\)
\(\Rightarrow\left|\overrightarrow{AH}\right|=AH=a\sqrt{3}\)
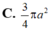
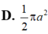
AI =√18.75
Vì AH là đường cao tam giác đều
nên BAH là tam giác nứa đều
nên AB=2BH=2,5
AD ĐL Pytago đc AH2=52-2,52=6,25
Vậy AH =2,5