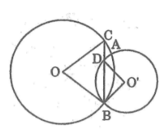
cho hai đường tròn tâm (O) ,(O') cắt nhau tại A và B .đường phân giác của góc OBO' cắt các đường tròn (O) ,(O') tương ứng tại C,D.Hãy so sánh các góc ở tâm BOC và BO'D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔOBC cân tại O nên \(\widehat{BOC}=180^0-2\cdot\widehat{OBC}\)
ΔBO'D cân tại O' nên \(\widehat{BO'D}=180^0-2\cdot\widehat{O'BD}\)
mà \(\widehat{OBC}=\widehat{O'BD}\)
nên \(\widehat{BOC}=\widehat{BO'D}\)

vì C, B cùng thuộc đường tròn (O) => OB=OC => tam giác OBC cân tại O => góc OCB= góc OBC (1)
tương tự góc O'BD= góc O'DB (2)
vì BD là tia pg của góc OBO' => góc OBC= góc DBO' (3)
từ (1) , (2) , (3)=> góc OBC=OCB=O'DB=O'BD
=> góc BOC = góc DO'B

a) Xét (O) có
DB là tiếp tuyến có B là tiếp điểm(gt)
DC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: DB=DC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: DB=DC(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD\(\perp\)BC(đpcm)
b) Xét (O) có
ΔEAB nội tiếp đường tròn(E,A,B cùng thuộc đường tròn (O))
AB là đường kính(gt)
Do đó: ΔEAB vuông tại E(Định lí)
\(\Leftrightarrow\)BE\(\perp\)AE tại E
hay BE\(\perp\)DA
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDBA vuông tại B có BE là đường cao ứng với cạnh huyền DA, ta được:
\(DE\cdot DA=DB^2\)(1)
Ta có: DO\(\perp\)BC(cmt)
mà DO cắt BC tại F(gt)
nên BF\(\perp\)DO tại F
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDBO vuông tại B có BF là đường cao ứng với cạnh huyền DO, ta được:
\(DF\cdot DO=DB^2\)(2)
Từ (1) và (2) suy ra \(DF\cdot DO=DE\cdot DA\)(đpcm)

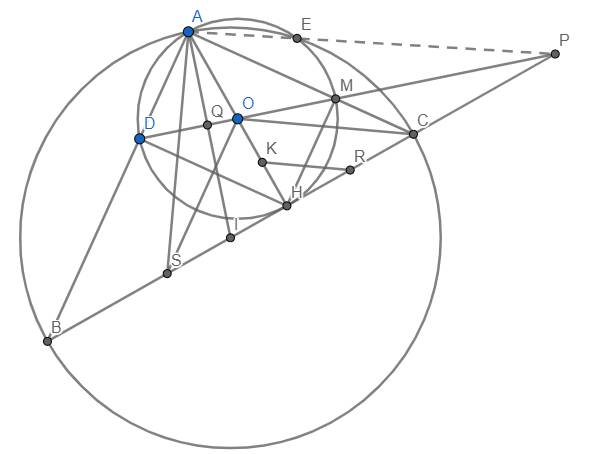
a) Chứng minh tam giác ABH vuông tại H và \(DH\perp AB\) rồi dùng hệ thức lượng \(\Rightarrow AD.AB=AH^2\). Tương tự, ta có \(AM.AC=AH^2\). Do đó \(AD.AB=AM.AC\) và theo bổ đề quen thuộc thì tứ giác BCMD nội tiếp. (đpcm)
b) Gọi Q là giao điểm của DM và AI. Khi đó tam giác ABC vuông tại A có trung tuyến AI nên \(IA=IB=IC=\dfrac{BC}{2}\) hay tam giác IBA cân tại I, suy ra \(\widehat{B}=\widehat{DAQ}\).
Lại có \(\widehat{B}+\widehat{ACB}=90^o\) suy ra \(\widehat{DAQ}+\widehat{ADQ}=90^o\) (do \(\widehat{ADQ}=\widehat{ACB}\) (cmt)). Do đó \(PQ\perp AI\) tại Q. Từ đó dễ dàng chứng minh O là trực tâm tam giác AIP.
c) Do tứ giác BCMD nội tiếp nên \(PM.PD=PC.PB\) \(\Rightarrow P_{P/\left(O\right)}=P_{P/\left(I\right)}\) \(\Rightarrow\) P nằm trên trục đẳng phương của (O) và (I). Lại có AE chính là trục đẳng phương của (O) và (I) nên A, E, P thẳng hàng. (đpcm)
d) Ta thấy SO//AB \(\perp AC\) và \(AH\perp BC\) nên O là trực tâm tam giác ASC \(\Rightarrow OC\perp AS\)
Lại có OC//KR nên \(RK\perp SA\) (đpcm)
Ở bài này chứng minh được \(A\in\left(I\right)\) vì BC là đường kính của (I) và \(\widehat{BAC}=90^o\)