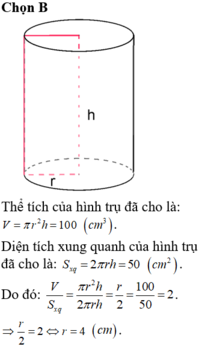
Một hình trụ có diện tích xung quanh là 80π cm2 và thể tích là 160π cm2.
Bán kính đáy của hình trụ này là R = ........... cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
4 tháng 7 2021
\(S_{xq}=140\pi\Leftrightarrow2\pi rh=140\pi\Leftrightarrow h=\dfrac{70}{r}\left(1\right)\)
\(S_{tp}=360\pi\Leftrightarrow2\pi r\left(r+h\right)=360\pi\Leftrightarrow r\left(r+h\right)=180\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow r\left(r+\dfrac{70}{r}\right)=180\\ \Leftrightarrow r^2+70=180\Rightarrow r=\sqrt{110}\)
4 tháng 7 2021
Tổng diện tích 2 đáy là:
\(360\pi-140\pi=220\pi\left(cm^2\right)\)
Bán kính đáy hình trụ là:
\(\sqrt{\dfrac{220\pi}{2\pi}}=\sqrt{110}\) (cm2)
CM
4 tháng 11 2019
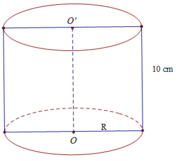
b) Thể tích hình trụ:
V = π R 2 h = π. 8 2 .10 = 640π ( c m 3 )
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Diện tích xung quanh hình trụ là:
$2\pi rh=90\Rightarrow \pi rh=45$ (cm2)
Thể tích hình trụ là:
$\pi r^2h=r.\pi rh=3.45=135$ (cm3)
9 tháng 5 2021
Ta có : \(S_{xq}=2\pi Rh=90\)
\(\Rightarrow h=\dfrac{90}{2\pi R}=\dfrac{15}{2\pi}\left(cm\right)\)
\(\Rightarrow V=\pi R^2h=\pi.3^2.\dfrac{15}{2\pi}=\dfrac{135}{2}\left(cm^3\right)\)
Vậy ...
30 tháng 6 2021
\(Sxq=2\pi Rh=>h=\dfrac{Sxq}{2\pi R}=\dfrac{352}{2.3,14.7}\approx8cm\)
RK
30 tháng 6 2021
Sxq= 2 \(\pi.r.h\)
\(\Leftrightarrow352\simeq2\cdot3,14\cdot7\cdot h\)
\(\Rightarrow\) h = \(8\left(cm\right)\)
17 tháng 6 2023
a: Chu vi đường tròn đáy là 192/24=8cm
R=8:2:3,14=1,27(cm)
b:V=24*1,27^2*3,14=121,55(cm3)
CM
29 tháng 1 2017
Đáp án A
Gọi chiều cao của hình trụ là h
Ta có:
S x q = 2 π R 2 h ⇔ 2 π . 5 2 . h = 300 π ⇒ h = 6 ( c m )
