cho a,b là hai số thực sao cho a*b>0 tìm giá trị nhỏ nhất của biểu thức A = (a+b)(1/a+1/b)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho a,b là hai số thực thõa mãn a.b>0
Khi đó, giá trị nhỏ nhất của biểu thức Q=(a+b)(1/a+1/b), Qmin=?

(a+b)(1/a+1/b)=1+a/b+b/a+1
=2+(a^2+b^2)/(a*b)
vì a^2+b^2>0; a*b>0
=>Qmin=2

Giả sử phương trình đã cho có 3 nghiệm
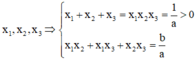
Khi đó
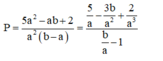
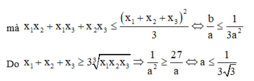
Suy ra
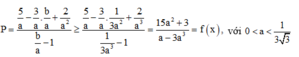
Xét hàm số:
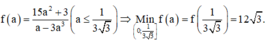
Chọn D.

từ giả thiết ta có
a+b+c=0
<=> a=-(b+c0
a2=b2 +c2 +2bc
tương tự b2=a2+c2+2ac
c2=a2+b2+2ab
thay vào Q ta đc
\(Q=\frac{1}{a^2+b^2-c^2}+\frac{1}{b^2+c^2-a^2}+\frac{1}{a^2+c^2-b^2}\)
\(Q=\frac{1}{a^2+b^2-a^2-b^2-2ab}+\frac{1}{b^2+c^2-b^2-c^2-2bc}+\frac{1}{a^2+c^2-a^2-c^2-2ac}\)
\(Q=\frac{-1}{2ab}-\frac{1}{2bc}-\frac{1}{2ac}\)
\(Q=\frac{-b-a-c}{2abc}\)
\(Q=\frac{-\left(a+b+c\right)}{2abc}\)
\(Q=0\)
Vậy với a,b,c khác 0, a+b+c=0 thì Q=0

Bạn nhân hai biểu thức rồi dùng bất đẳng thức cô-si.suy ra min=4

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
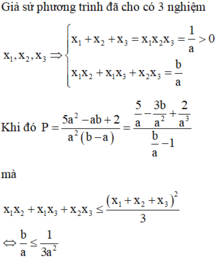
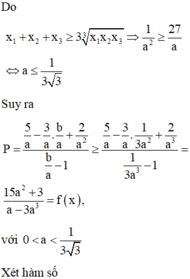
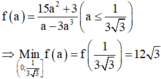
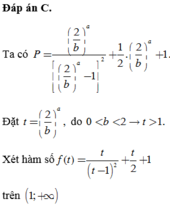
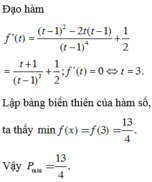
kết quả chắc chắn 100 phần trăm là =1 đó
Giá trị nhỏ nhất của biểu thức \(A_{min}=4\)