cứu em Giá trị nhỏ nhất của A= x2 -24x+145 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
16 tháng 12 2022
Vì \(x^2 \ge 0\) với mọi `x`
\(=>x^{2}+2021 \ge 2021\) với mọi `x`
Hay \(A \ge 2021\) với mọi `x`
Dấu "`=`" xảy ra `<=>x=0`
CM
17 tháng 12 2017
Xét hàm số
f x = x 3 - 9 x 2 + 24 x - 68 f ' x = 3 x 2 - 18 x + 24 = 0 ⇔ x = 2 x = 4
Ta có f(-1) = -102; f(2) = -48; f(4) = -52.
Do đó 102 ≤ f x ≤ - 48 . Suy ra 48 ≤ f x ≤ 102 .
Vậy m = 48; M = 102 hay m M = 8 17
Đáp án B
VT
0
G
1
18 tháng 1 2023
\(A=5x^2+9y^2-12xy+24x-48y+81\)
\(A=4x^2+x^2+9y^2-12xy+32x-48y-8x+16+1+64\)
\(A=(4x^2+9y^2+64-12xy+32x-48y)+\left(x^2-8x+16\right)+1\)
\(A=[\left(2x\right)^2+\left(3y\right)^2+\left(8\right)^2-2.2x.3y-2.3y.8+2.2x.8]+\left(x^2-8x+16\right)+1\)
\(A=\left(2x-3y+8\right)^2\left(x-4\right)^2+1\)
\(Do\) \(\left(2x-3y+8\right)^2\ge0\) \(và\) \(\left(x-4\right)^2\ge0\)
\(\Rightarrow A_{min}=1\)
CM
2 tháng 10 2019
Chọn C
Hàm số y =
x
2
+
x
+
4
x
+
1
là hàm phân thức có tập xác định là 
nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
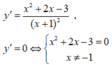
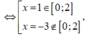
Ta có 
=> A = 4, a = 3.
Vậy a + A = 7.
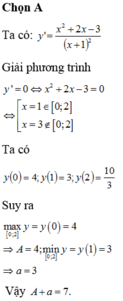
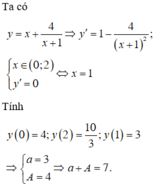
\(A\ge1\forall x\)
Dấu '=' xảy ra khi x=12
\(A=x^2-24x+144+1=\left(x-12\right)^2+1\ge1\\ A_{min}=1\Leftrightarrow x=12\)