Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, gọi M là trung điểm của AB. Trên tia đối của tia MH lấy điểm D sao cho MD = MH. a) Chứng minh : tứ giác AHBD là hình chữ nhật. b) Gọi E là điểm đối xứng của B qua điểm H. Chứng minh tứ giác ADHE là hình bình hành. c)Gọi N là giao điểm của AH và DE,K là trung điểm AC.Chứng minh MN//BC và 3 điểm M,N,K thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2022
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Xét ΔAEB có
H là trung điểm của EB
M là trung điểm của AB
Do đó: HM là đường trung bình
=>HM//AE và HM=AE/2
hay HD//AE và HD=AE
hay ADHE là hình bình hành
CH
Cô Hoàng Huyền
Admin
VIP
13 tháng 12 2017
a) Xét tứ giác AHBD có MB = MA; MD = MH nên nó là hình bình hành (dhnb).
Lại có \(\widehat{BHA}=90^o\) nên AHBD là hình chữ nhật (dhnb).
b) Do AHBD là hình chữ nhật nên AD song song và bằng HB.
Lại có HB = HE nên AD song song và bằng HE.
Xét tứ giác ADHE có AD song song và bằng HE nên nó là hình bình hành (dhnb)
c) Lấy J là trung điểm AF.
Do AB và EF cùng vuông góc với AC nên BAFE là hình thang vuông.
Lại có H, J là trung điểm các cạnh bên nên HJ là đường trung bình của hình thang.
Vậy nên HJ // AB // EF hay \(HJ\perp AF\)
Xét tam giác AHF có HJ là trung tuyến đồng thời đường cao nên nó là tam giác cân.
Vậy thì HA = HF.
d) Xét tam giác vuông EFC có FI là trung tuyến ứng với cạnh huyền nên FI = IC hay \(\widehat{IFC}=\widehat{ICF}\)
Lại có \(\widehat{ICF}=\widehat{BAH}\) (Cùng phụ với góc HAC)
Nên \(\widehat{IFC}=\widehat{BAH}\)
Ta cũng có \(\widehat{HFE}=\widehat{JHF}\) (Hai góc so le trong)
\(\widehat{JHF}=\widehat{JHA}\) (HJ là phân giác)
\(\widehat{JHA}=\widehat{BAH}\) (Hai góc so le trong)
nên \(\widehat{HFE}=\widehat{BAH}\)
Vậy thì \(\widehat{IFC}=\widehat{HFE}\)
Từ đó ta có : \(\widehat{IFC}+\widehat{EFI}=\widehat{HFE}+\widehat{EFI}\Rightarrow\widehat{HFI}=\widehat{EFC}=90^o\)
Hay \(HF\perp FI\)
20 tháng 12 2022
a: Xét tứ giác ADCH có
M là trung điểm chung của AC và HD
góc AHC=90 độ
Do đó: ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
Do đó: ADHE là hình bình hành
17 tháng 3 2023
a: Xét tứ giác AHCD có
M là trung điểm chung của AC và HD
góc AHC=90 độ
=>AHCD là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
=>ADHE là hình bình hành
16 tháng 12 2022
Sửa đề; N là giao của ED và AH
a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
DO đó; AHBDlà hình chữ nhật
b: Xét tứ giác AEHD có
AD//EH
AD=EH
Do đó:AEHD là hình bình hành
=>AH cắt ED tại trung điểm của mỗi đường
=>N là trung điểm của AH
c: Xét ΔAHB có AM/AB=AH/AH
nên MN//HB
=>MN//BC
Xét ΔABC có AM/AB=AK/AC
nên MK//BC
mà MN//BC
nên M,N,K thẳng hàng
17 tháng 12 2021
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{HAB}=90^0\)
nên AHBD là hình chữ nhật
16 tháng 12 2023
a: Xét tứ giác AHBD có
O là trung điểm chung của AB và HD
=>AHBD là hình bình hành
Hình bình hành AHBD có \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Ta có: AHBD là hình chữ nhật
=>AH//BD và AH=BD
Ta có: AH//BD
Q\(\in\)AH
Do đó: QH//DB
Ta có: AH=BD
AH=HQ
Do đó: BD=HQ
Xét tứ giác BDHQ có
BD//HQ
BD=HQ
Do đó: BDHQ là hình bình hành
c: Xét tứ giác ABQP có
H là trung điểm chung của AQ và BP
=>ABQP là hình bình hành
Hình bình hành ABQP có AQ\(\perp\)BP
nên ABQP là hình thoi
d: Ta có: ΔKAB vuông tại K
mà KO là đường trung tuyến
nên \(KO=\dfrac{AB}{2}\)
mà AB=HD(AHBD là hình chữ nhật)
nên \(KO=\dfrac{HD}{2}\)
Xét ΔKHD có
KO là đường trung tuyến
\(KO=\dfrac{HD}{2}\)
Do đó: ΔKHD vuông tại K
=>KH\(\perp\)KD
8 tháng 10 2023
a: Xét tứ giác AHCD có
M là trung điểm chung của AC và HD
\(\widehat{AHC}=90^0\)
Do đó: AHCD là hình chữ nhật
b: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔABC có
H,M lần lượt là trung điểm của CB,CA
=>HM làđường trung bình
=>HM//AB và HM=AB/2
mà HM=HD/2
nên AB=HD
c:
AHCD là hình bình hành
=>AD//CH và AD=CH
AD//CH
=>AD//BH
AD=CH
CH=BH
Do đó: AD=BH
Xét tứ giác ABHD có
AD//BH
AD=BH
Do đó: ABHD là hình bình hành
KV
29 tháng 12 2023
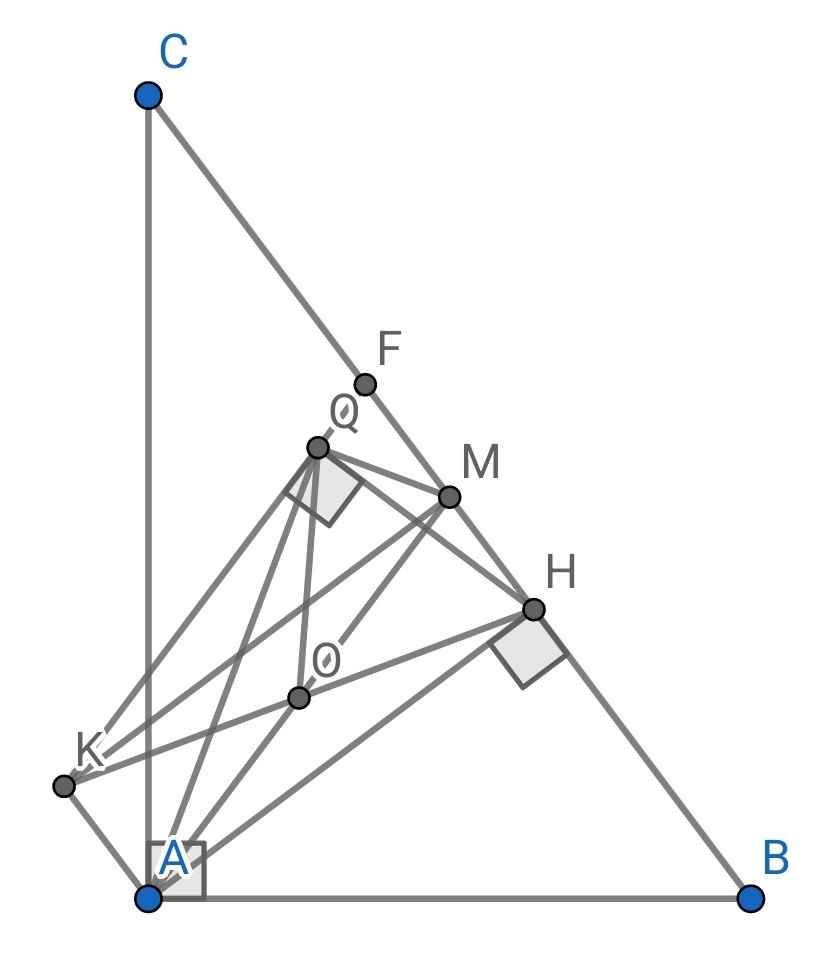a) Do OH = OK (gt)
⇒ O là trung điểm của KH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ AH ⊥ HM
⇒ ∠AHM = 90⁰
Tứ giác AHMK có:
O là trung điểm của AM (gt)
O là trung điểm của KH (cmt)
⇒ AHMK là hình bình hành
Mà ∠AHM = 90⁰ (cmt)
⇒ AHMK là hình chữ nhật
b) Do AHMK là hình chữ nhật (cmt)
⇒ AK = MH và AK // MH
Do MF = MH (gt)
⇒ AK = MF
Do AK // MH (cmt)
⇒ AK // MF
Tứ giác AMFK có:
AK // MF (cmt)
AK = MF (cmt)
⇒ AMFK là hình bình hành
c) Do AHMK là hình chữ nhật (cmt)
⇒ OA = OH = OM = OK = AM : 2
∆HQK vuông tại Q có OQ là đường trung tuyến
⇒ OQ = OH = HK : 2
Mà OH = OM = OA (cmt)
⇒ OQ = OM = OA = AM : 2
∆AQM có:
OQ là đường trung tuyến (do O là trung điểm của AM)
Mà OQ = OA = OM = AM : 2 (cmt)
⇒ ∆AQM vuông tại Q
⇒ MQ ⊥ AQ
\(a,\) Vì M là trung điểm AB cà DH nên AHBD là hình bình hành
Mà \(\widehat{AHB}=90^0\) (đường cao AH) nên AHBD là hcn
\(b,\) Vì AHBD là hcn nên \(AD=BH;AD\text{//}HB\)
Mà \(BH=HE\Rightarrow AD=HE;AD\text{//}HE\)
Do đó: ADHE là hình bình hành
\(c,\) Vì ADHE là hbh mà N là giao AH và DE nên N là trung điểm AH và DE
Mà M là trung điểm AB nên MN là đtb \(\Delta ABH\)
Do đó \(MN//BH\) hay \(MN//BC\)
Ta có N là trung điểm AH và K là trung điểm AC nên NK là đtb \(\Delta ACH\)
Do đó \(NK//HC\) hay \(NK//BC\)
Do đó theo định lí Ta lét thì MN trùng NK hay M,N,K thẳng hàng
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật