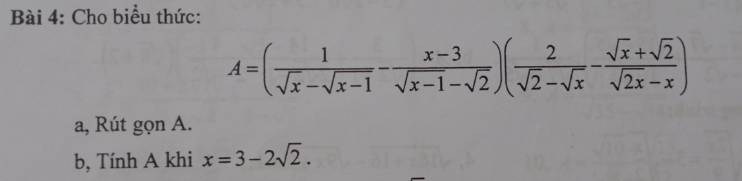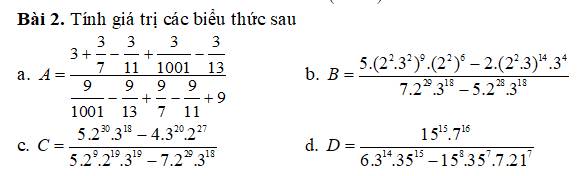em cần trước 10h ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 . i wish my mother was here to help me with my homework
2. lan said her brother often travelled abroad with her father.
3 the teacher asked mai if she bought a new calculator
4 it was very generous of john to give them 100
5 if you don't ride a bike fast, you will go to school late
6 it is very important for athletes to be in good health
7 has just made
8 were
9 was having
10 meeting

Bài trên:
\(16x^3y+0,25yz^3=\dfrac{1}{4}y\left(64x^3+z^3\right)=\dfrac{1}{4}y\left[\left(4x\right)^3+z^3\right]\\ =\dfrac{1}{4}y\left[\left(4x+z\right)\left(16x^2-4xz+z^2\right)\right]\\ ----\\ x^4-4x^3+4x^2=x^2\left(x^2-4x+4\right)=x^2\left(x-2\right)^2\\ -----\\ a^3+a^2b-ab^2-b^3=\left(a^3-b^3\right)+\left(a^2b-ab^2\right)\\ =\left(a-b\right)\left(a^2+ab+b^2\right)+ab\left(a-b\right)=\left(a-b\right)\left(a^2+2ab+b^2\right)=\left(a-b\right)\left(a+b\right)^2\)
Bài trên
\(x^3+x^2-4x-4\\ =x^2\left(x+1\right)-4\left(x+1\right)\\ =\left(x^2-4\right)\left(x+1\right)\\ =\left(x-2\right)\left(x+2\right)\left(x+1\right)\\ ---\\ x^3-x^2-x+1\\ =x^2\left(x-1\right)-\left(x-1\right)\\ =\left(x^2-1\right)\left(x-1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x-1\right)=\left(x-1\right)^2\left(x+1\right)\\ ---\\ x^4+x^3+x^2-1\\ =x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)\\ =\left(x^3+x-1\right)\left(x+1\right)\\ ---\\ x^2y^2+1-x^2-y^2\\ =x^2.\left(y^2-1\right)-\left(y^2-1\right)\\ =\left(y^2-1\right)\left(x^2-1\right)\\ =\left(y-1\right)\left(y+1\right)\left(x-1\right)\left(x+1\right)\)

1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)

Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.

\(A=\left(\dfrac{1}{\sqrt{x}-\sqrt{x-1}}-\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\right)\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{2x}-x}\right)\) (ĐK: \(x\ge1,x\ne2,x\ne3\))
\(A=\left[\dfrac{\sqrt{x}+\sqrt{x-1}}{\left(\sqrt{x}-\sqrt{x-1}\right)\left(\sqrt{x}+\sqrt{x-1}\right)}-\dfrac{\left(x-3\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{\left(\sqrt{x-1}-\sqrt{2}\right)\left(\sqrt{x-1}+\sqrt{2}\right)}\right]\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)
\(A=\left[\dfrac{\sqrt{x}+\sqrt{x-1}}{x-x+1}-\dfrac{\left(x-3\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{x-1-2}\right]\left[\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right]\)
\(A=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(A=\left(\sqrt{x}-\sqrt{2}\right)\cdot-\dfrac{1}{\sqrt{x}}\)
\(A=\dfrac{\sqrt{2}-\sqrt{x}}{\sqrt{x}}\)
b) Ta có: \(x=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2=\left(\sqrt{2}-1\right)^2\)
Thay vào A ta có:
\(A=\dfrac{\sqrt{2}-\sqrt{\left(\sqrt{2}-1\right)^2}}{\sqrt{\left(\sqrt{2}-1\right)^2}}=\dfrac{\sqrt{2}-\sqrt{2}+1}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)

1. - Nồi nhôm,khung cửa nhôm, thau nhôm
- Cửa sắt, kéo bằng thép, bồn rửa chén bằng sắt.
- Thau nhựa, ống nước, ghế nhựa.
2. Kẹo hóa học, đường hóa học, thuốc trừ sâu.
3. Thuốc giảm đau, thuốc gây tê, thuốc gây mê, xi măng,...
4. Hộp bút, thước dẻo, bảng đen,...

\(a,A=\dfrac{3+\dfrac{3}{7}-\dfrac{3}{11}+\dfrac{3}{1001}-\dfrac{3}{13}}{\dfrac{9}{1001}-\dfrac{9}{13}+\dfrac{9}{7}-\dfrac{9}{11}+9}\)
\(=\dfrac{3+\dfrac{3}{7}-\dfrac{3}{11}+\dfrac{3}{1001}-\dfrac{3}{13}}{9+\dfrac{9}{7}-\dfrac{9}{11}+\dfrac{9}{1001}-\dfrac{9}{13}}\)
\(=\dfrac{3\cdot\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{1001}-\dfrac{1}{13}\right)}{9\cdot\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{1001}-\dfrac{1}{13}\right)}\)
\(=\dfrac{3}{9}\)
\(=\dfrac{1}{3}\)
\(---\)
\(b,B=\dfrac{5\cdot\left(2^2\cdot3^2\right)^9\cdot\left(2^2\right)^6-2\cdot\left(2^2\cdot3\right)^{14}\cdot3^4}{7\cdot2^{29}\cdot3^{18}-5\cdot2^{28}\cdot3^{18}}\)
\(=\dfrac{5\cdot2^{18}\cdot3^{18}\cdot2^{12}-2\cdot2^{28}\cdot3^{14}\cdot3^4}{2^{28}\cdot3^{18}\cdot\left(7\cdot2-5\right)}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-2^{29}\cdot3^{18}}{2^{28}\cdot3^{18}\cdot\left(14-5\right)}\)
\(=\dfrac{2^{29}\cdot3^{18}\cdot\left(5\cdot2-1\right)}{2^{28}\cdot3^{18}\cdot9}\)
\(=\dfrac{2\cdot\left(10-1\right)}{9}\)
\(=\dfrac{2\cdot9}{9}\)
\(=2\)
\(---\)
\(c,C=\dfrac{5\cdot2^{30}\cdot3^{18}-4\cdot3^{20}\cdot2^{27}}{5\cdot2^9\cdot2^{19}\cdot3^{19}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-2^2\cdot3^{20}\cdot2^{27}}{5\cdot2^{28}\cdot3^{19}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-2^{29}\cdot3^{20}}{2^{28}\cdot3^{18}\cdot\left(5\cdot3-7\cdot2\right)}\)
\(=\dfrac{2^{29}\cdot3^{18}\cdot\left(5\cdot2-3^2\right)}{2^{28}\cdot3^{18}\cdot\left(15-14\right)}\)
\(=\dfrac{2\cdot\left(10-9\right)}{1}\)
\(=2\)
\(---\)
\(d,D=\dfrac{15^{15}\cdot7^{16}}{6\cdot3^{14}\cdot35^{15}-15^8\cdot35^7\cdot7\cdot21^7}\)
\(=\dfrac{\left(3\cdot5\right)^{15}\cdot7^{16}}{2\cdot3\cdot3^{14}\cdot\left(5\cdot7\right)^{15}-\left(3\cdot5\right)^8\cdot\left(5\cdot7\right)^7\cdot7\cdot\left(3\cdot7\right)^7}\)
\(=\dfrac{3^{15}\cdot5^{15}\cdot7^{16}}{2\cdot3^{15}\cdot5^{15}\cdot7^{15}-3^8\cdot5^8\cdot5^7\cdot7^7\cdot7\cdot3^7\cdot7^7}\)
\(=\dfrac{3^{15}\cdot5^{15}\cdot7^{16}}{2\cdot3^{15}\cdot5^{15}\cdot7^{15}-3^{15}\cdot5^{15}\cdot7^{15}}\)
\(=\dfrac{3^{15}\cdot5^{15}\cdot7^{16}}{3^{15}\cdot5^{15}\cdot7^{15}\cdot\left(2-1\right)}\)
\(=\dfrac{7}{1}\)
\(=7\)
#\(Toru\)

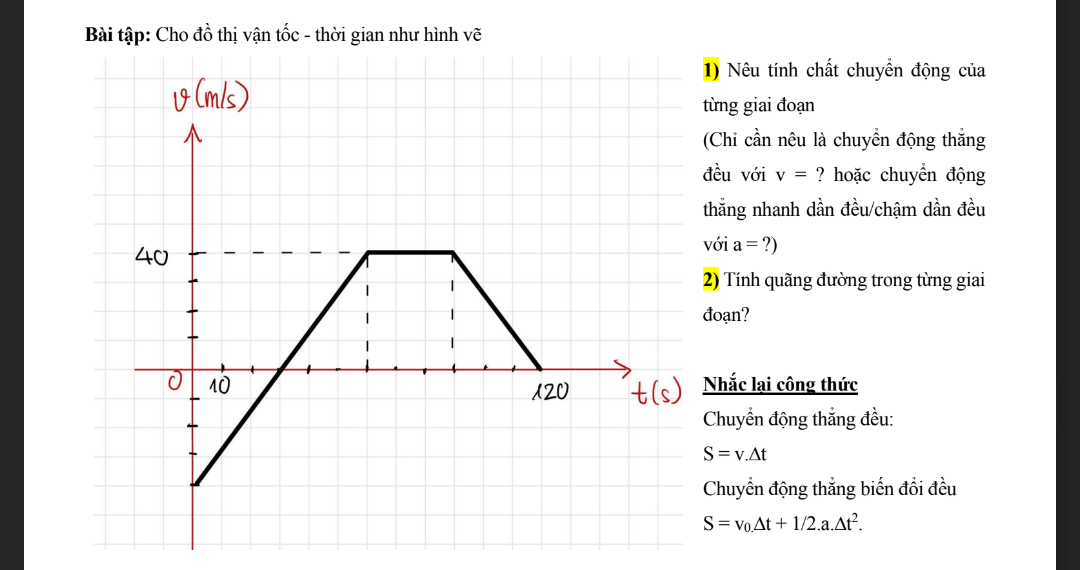
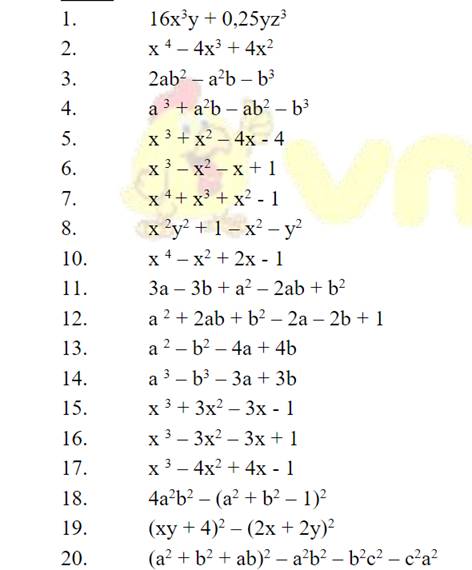
 giúp tui với ạ trước 10h nha tui đang cần gấp
giúp tui với ạ trước 10h nha tui đang cần gấp