 GGiup e bài 4 nữa nha mọi người
GGiup e bài 4 nữa nha mọi người
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHD có
AP là đường cao ứng với cạnh HD
AP là đường trung tuyến ứng với cạnh HD
Do đó: ΔAHD cân tại A
mà AP là đường cao ứng với cạnh HD
nên AP là đường phân giác ứng với cạnh HD
Xét ΔAHE có
AQ là đường cao ứng với cạnh HE
AQ là đường trung tuyến ứng với cạnh HE
Do đó: ΔHAE cân tại A
mà AQ là đường cao ứng với cạnh HE
nên AQ là đường phân giác ứng với cạnh HE
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của DE
a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)
góc APD = APH=90o
AD = AH
AP chung
=> AD=AH (1)
CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)
=> AE= AH (2)
Từ 1 và 2 => AD= AE
=> A là trung điểm của DE
b) Xét \(\Delta DHE\) có:
DP=PH; HQ=QE
=> PQ là đg trung bình của tam giắc DHE
=> PQ// DE; PQ=1/2 DE
c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o
=> Tứ giác APHQ là HCN
=> PQ=AH ( theo t/c HCN)

Bài 2:
a: Xét ΔBDC có
M là trung điểm của BC
ME//BD
Do đó: E là trung điểm của DC
Suy ra: DE=EC(1)
Xét ΔAME có
I là trung điểm của AM
ID//ME
Do đó: D là trung điểm của AE
Suy ra: AD=DE(2)
Từ (1) và (2) suy ra AD=DE=EC

Ờ thì giúp tội tui ko tên thắng :))
Ta có: \(a+b+c=\sqrt{\left(a+b+c\right)^2}\)
\(=\sqrt{a^2+b^2+c^2+2ab+2bc+2ca}\ge\sqrt{3\left(ab+bc+ca\right)}=3\)
Sau đó áp dụng BĐT AM-GM và Holder ta có:
\(Σ\dfrac{a^2}{\sqrt{3b^2+bc}}=Σ\dfrac{4a^2}{2\sqrt{4b\left(3b+c\right)}}\geΣ\dfrac{4a^2}{7b+c}\)
\(=Σ\dfrac{4a^3}{7ab+ac}\ge\dfrac{4\left(a+b+c\right)^3}{3Σ\left(7ab+ac\right)}=\dfrac{\left(a+b+c\right)^3}{18}\ge\dfrac{3}{2}\)
Xảy ra khi \(a=b=c=1\)
Never nerf :|, cũng xài Holder nhưng theo hướng khác :v
Áp dụng BĐT Holder ta có:
Đặt \(P=\dfrac{a^2}{\sqrt{3b^2+bc}}+\dfrac{b^2}{\sqrt{3c^2+ca}}+\dfrac{c^2}{\sqrt{3a^2+ab}}\)
\(P^2\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\ge\left(a^2+b^2+c^2\right)^3\)
Giờ chứng minh \(\left(a^2+b^2+c^2\right)^3\ge\dfrac{9}{4}\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)
\(\Leftrightarrow4\left(a^2+b^2+c^2\right)^3\ge9\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)
\(\Leftrightarrow4\left(a^2+b^2+c^2\right)^3\ge3\left(ab+bc+ca\right)\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)
Lại có BĐT quen thuộc \(a^2+b^2+c^2\ge ab+bc+ca\)
Nên chỉ ra \(4\left(a^2+b^2+c^2\right)^2\ge3\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)
Điều này đúng vì
\(4\left(a^2+b^2+c^2\right)^2\ge12\left(a^2b^2+b^2c^2+c^2a^2\right)=3\left(4a^2b^2+4b^2c^2+4c^2a^2\right)\)
\(\ge3\left(3a^2b^2+a^2bc+3b^2c^2+ab^2c+3c^2a^2+abc^2\right)\)
\(=3\left[a^2\left(3b^2+bc\right)+b^2\left(3c^2+ca\right)+c^2\left(3a^2+ab\right)\right]\)

Overcrowding is a pressing issue that affects many communities around the world. It refers to a situation where the number of people living in a particular area exceeds its capacity. This can occur due to rapid population growth, urbanization, and migration, coupled with insufficient housing infrastructure. The effects of overcrowding are far-reaching and detrimental. Firstly, it poses significant health risks as it increases the likelihood of the spread of diseases. Additionally, overcrowded areas often experience higher crime rates, as the lack of space and resources can lead to heightened tensions. Moreover, overcrowding puts a strain on public services and resources, such as schools, hospitals, and transportation systems. To address this issue, it is crucial to implement effective urban planning and development strategies, along with initiatives to provide affordable housing. Furthermore, improving transportation systems can help distribute the population more evenly. Lastly, population control measures should be considered to manage the growth rate. In conclusion, overcrowding is a complex problem that requires collective efforts from individuals and governments. By taking proactive steps, we can create healthier and more sustainable communities for future generations.
$HaNa♬☘$



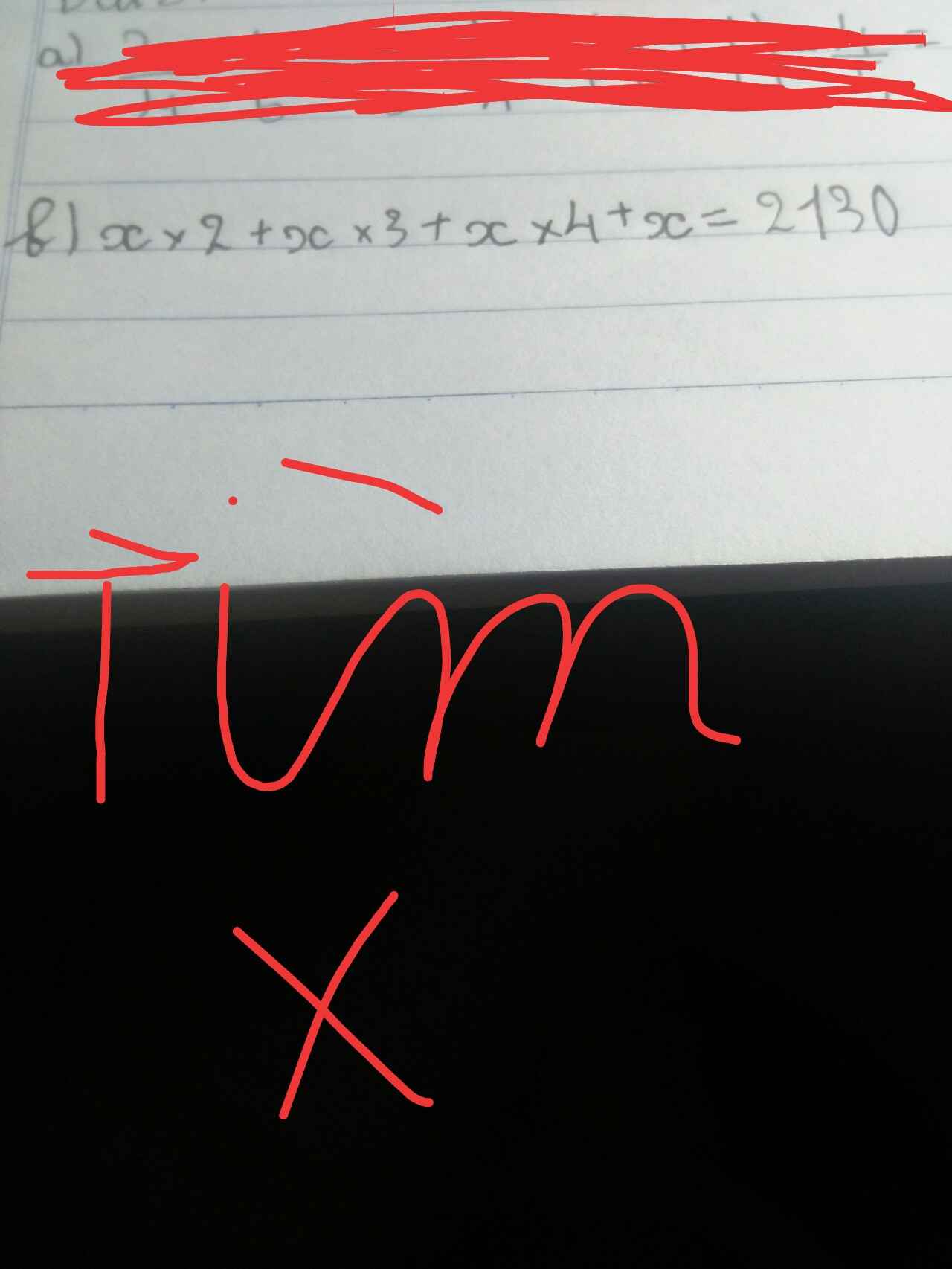

 ggiup nhé thắng
ggiup nhé thắng
4) BÀI GIẢI :
Số đồ chơi Hải làm được là :
12 x 3 = 36 ( đồ chơi )
Số đồ chơi cả hai bạn làm là :
36 + 12 = 48 ( đồ chơi )
Đáp số : 38 đồ chơi bạn nhé