Giữa 2 điểm AB người ta đặt hiệu điện thế không đổi là 36V.Trong đó có mắc song song hai điện trở R1=40ôm R2=60ôm A:tính điện trở tương đương của đoạn mạch B:tính cường độ dòng điện qua mỗi điện trở và mạch chính C: tính công suất tiêu thụ của đoạn mạch D:mắc thêm bóng đèn Đ(22V-24W)nối tiếp với đoạn mạch trên.đèn có sang bình thường không?tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2022
Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{30.60}{30+60}=20\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=30V\)
Cường độ dòng điện chạy qua mạch chính và mỗi mạch rẽ:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{30}{20}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{30}{30}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{30}{60}=0,5\left(A\right)\end{matrix}\right.\)
Điện trở tương đương lúc này là:
\(R_{tđ}=R_{12}+R_3=20+40=60\left(\Omega\right)\)
Do mắc nối tiếp nên \(I=I_{12}=I_3=1,5\left(A\right)\)
Nhiệt năng đoạn mạch tiêu thụ trong 30ph:
\(A=P.t=I^2.R.t=1,5^2.60.30.60=243000\left(J\right)\)
Nhiệt lượng tỏa ra của R3 trong 30ph:
\(Q_{tỏa_3}=A_3=I_3^2.R_3.t=1,5^2.40.30.60=162000\left(J\right)\)
27 tháng 8 2021
R1//R2
a,\(=>Rtd=\dfrac{R1R2}{R1+R2}=\dfrac{8.12}{8+12}=4,8\Omega\)
\(=>I1=\dfrac{U}{R1}=\dfrac{24}{8}=3A=>I2=\dfrac{U}{R2}=\dfrac{24}{12}=2A\)
b,\(=>Pab=U.Im=24\left(I1+I2\right)=24.5=120W\)
\(=>A=UIt=24.5.12.60=86400J\)
c,\(=>R1=\dfrac{pl}{S}=>l1=\dfrac{R1S}{p}=\dfrac{8.6.10^{-7}}{0,5.10^{-6}}=9,6m\)
d, R1 nt R2 nt R3
\(=>Im=\dfrac{U}{R1+R2+R3}=\dfrac{24}{25}A\)
23 tháng 12 2021
a) Điện trở tương đương của đoạn mạch AB:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Do mắc song song nên \(U=U_1=U_2=10V\)
Cường độ dòng điện qua mỗi điện trở:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{10}{24}=\dfrac{5}{12}\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{10}{60}=\dfrac{1}{6}\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{10}{40}=\dfrac{1}{4}\left(A\right)\end{matrix}\right.\)
26 tháng 9 2021
Điện trở tương đương của mạch:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\Leftrightarrow R_{tđ}=\dfrac{R_1R_2R_3}{R_1R_2+R_2R_3+R_3R_1}=\dfrac{4.6.12}{4.6+6.12+12.4}=2\Omega\)
CĐDĐ qua mỗi điện trở
\(I_1=\dfrac{U_1}{R_1}=\dfrac{U}{R_1}=\dfrac{4}{4}=1\left(A\right);\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{U}{R_2}=\dfrac{4}{6}=\dfrac{2}{3}\approx0,667\left(A\right);\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{U}{R_3}=\dfrac{4}{12}=\dfrac{1}{3}\approx0,333\left(A\right)\)
3 tháng 1 2022
Điện trở tương đương của đoạn mạch:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12.24}{12+24}=8\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=12V\)
Cường độ dòng điện chạy qua mỗi điện trở và qua mạch chính:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{12}{8}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{12}{12}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{24}=0,5\left(A\right)\end{matrix}\right.\)
N
1 tháng 11 2021
a. \(R=R1+R2=40+60=100\left(\Omega\right)\)
b + c. \(I=I1=I2=2,2A\left(R1ntR2\right)\)
\(\left[{}\begin{matrix}U=IR=2,2.100=220\left(V\right)\\U1=I1.R1=2,2.40=88\left(V\right)\\U2=I2.R2=2,2.60=132\left(V\right)\end{matrix}\right.\)
TK
1 tháng 11 2021
MCD R1 nt R2
a,Điện trở tương đương của đoạn mạch
\(R_{tđ}=R_1+R_2=40+60=100\left(\Omega\right)\)
b,Hiệu điện thế giữa 2 đầu đoạn mạch
\(U=R\cdot I=100\cdot2,2=220\left(V\right)\)
c,Hiệu điện thế giữa 2 đầu mỗi điện trở
\(I_1=I_2=I=2,2\left(A\right)\)
\(U_1=R_1I_1=40\cdot2,2=88\left(V\right)\)
\(U_2=I_2R_2=2,2\cdot60=132\left(V\right)\)
20 tháng 12 2021
a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{20.20}{20+30}=12\left(\Omega\right)\)
b) Có : \(U=U_1=U_2=12\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện qua các điện trở và qua mạch chính :
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{12}{20}=0,6\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{30}=0,4\left(A\right)\\I_{AB}=I_1+I_2=0,6+0,4=1\left(A\right)\end{matrix}\right.\)
c) 10 phút = 600s
Nhiệt lượng tỏa ra trên điện trở R1
\(Q_1=UIt=12.0,6.600=4320\left(J\right)\)
Chúc bạn học tốt
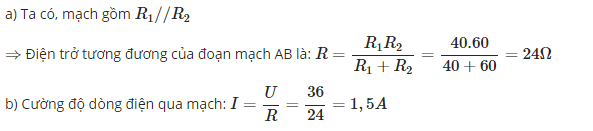
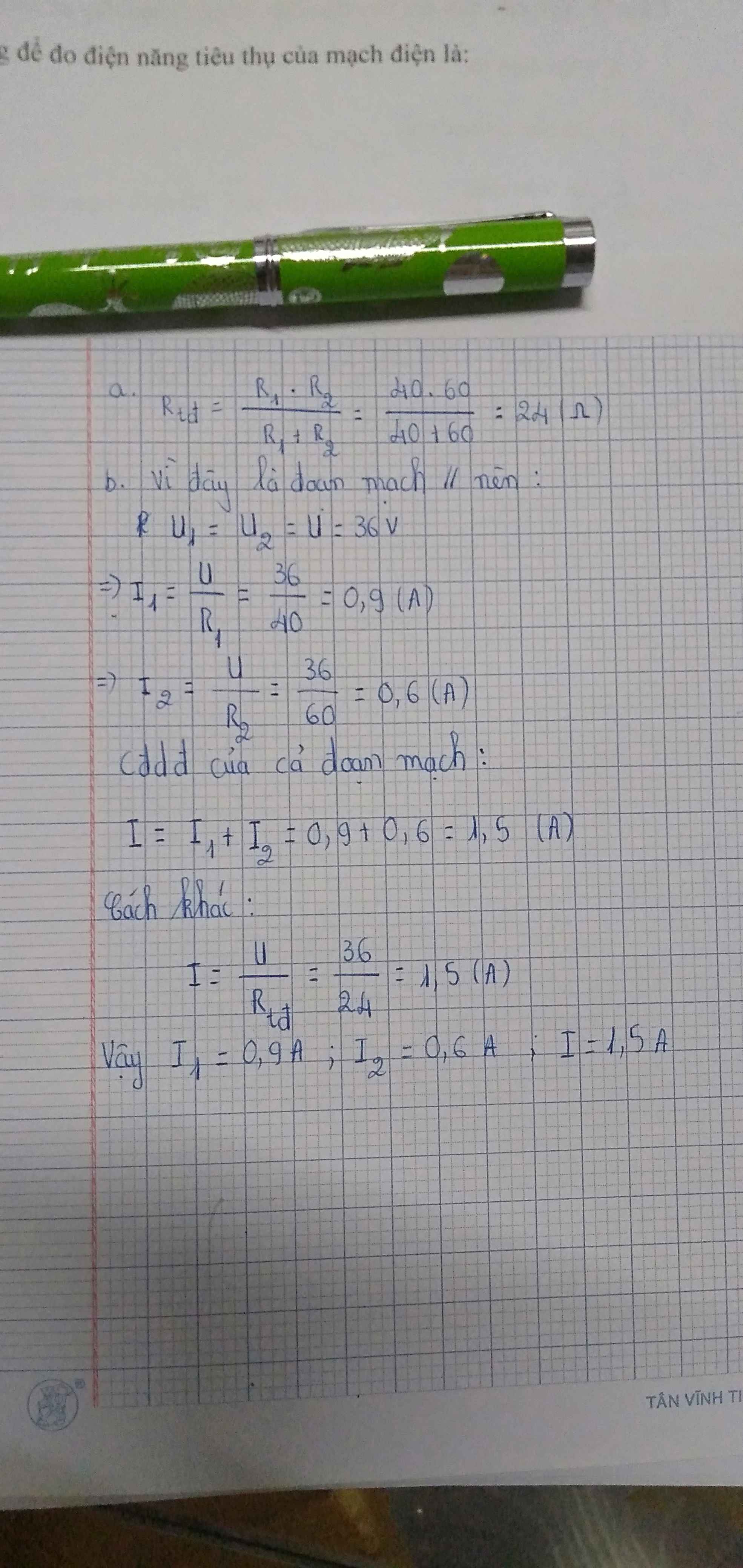
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{40.60}{40+60}=24\left(\Omega\right)\)
\(U=U_1=U_2=36V\)
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{36}{24}=\dfrac{3}{2}\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{36}{40}=\dfrac{9}{10}\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{36}{60}=\dfrac{3}{5}\left(A\right)\end{matrix}\right.\)
\(P=U.I=\dfrac{3}{2}.36=54\left(W\right)\)