Biết x;y;z>0 thỏa mãn:\(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}=1\) Khi đó giá trị nhỏ nhất của \(A=\frac{x^2}{x+y}+\frac{y^2}{y+z}+\frac{z^2}{z+x}\) là
(Nhập kết quả dưới dạng số thập phân gọn nhất)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
14 tháng 11 2021
b) Thay x=-28
\(\left(-2\right)+17+\left(-28\right)=-13\)
c) Thay x=-4
\(\left(-4\right)+25+\left(-47\right)=-26\)
d) Thay x=8
\(25+8+\left(-13\right)=20\)
19 tháng 11 2021
\(a,x+\left(-12\right)=\left(-24\right)+\left(-12\right)=-36\\ b,\left(-234\right)+y=\left(-234\right)+\left(-145\right)=-379\\ c,x+\left(-12\right)+\left(-234\right)=\left(-1\right)+\left(-12\right)+\left(-234\right)=-247\)
JS
2
1 tháng 12 2021
\(a,123:x+12:x=4,5\\ \Rightarrow\left(123+12\right):x=4,5\\ \Rightarrow135:x=4,5\\ \Rightarrow x=30\\ b,89:x-5,15:x=62,5\\ \Rightarrow\left(89-5,15\right):x=62,5\\ \Rightarrow83,85:x=62,5\\ \Rightarrow x=1,3416\)
B
23 tháng 11 2019
(1) Tìm x thuộc N biết 18 chia hết cho x khi x-2
Để 18 chia hết cho x khi x-2
=> 18 chia hết cho x-2
=> x-2 thuộc Ư(18) = {1;2;3;6;9;18}
Ta có bảng:
| x-2 | 1 | 2 | 3 | 6 | 9 | 18 |
| x | 3 | 4 | 5 | 8 | 11 | 20 |
Vậy x thuộc {3;4;5;8;11;20}
(2) Tìm x thuộc N biết x-1 chia hết cho 13
Để x-1 chia hết cho 13 => x-1 thuộc B(13) = {0;13;26;49;...}
=> x thuộc {1;14;27;30;...}
(3) Tìm x thuộc N biết x+10 chia hết cho x-2
Để x+10 chia hết cho x-2
=> (x-2)+12 chia hết cho x-2
Mà x-2 chia hết cho x-2
=> x-2 thuộc Ư(12) = {1;2;3;4;6;12}
Ta có bảng:
| x-2 | 1 | 2 | 3 | 4 | 6 | 12 |
| x | 3 | 4 | 5 | 6 | 8 | 14 |
Vậy x thuộc {3;4;5;6;8;14}
15 tháng 10 2015
Bài 1:
\(\frac{x+7}{x}=9\Rightarrow x+7=9x\Rightarrow9x-x=7\Rightarrow8x=7\Rightarrow x=\frac{7}{8}\)
Bài 2:
12,31; 12,32; 12,34
PT
1
25 tháng 12 2022
a, x có thể bằng: 4,21; 4,22; 4,23; 4,24; 4,25;...; 4,29
b, x có thể bằng: 5,611;...; 5,619
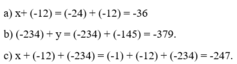
Ta có ... x = y = z = 1/3
thay vào ta có A = 0,5
Thần Đồng Đất Việt giải chi tiết cho mk đi bạn