Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
4 tháng 7 2017
Lời giải:
Ta có \(F(x)=\int \sin xe^{\cos x}dx=-\int e^{\cos x}d(\cos x)\)
\(\Leftrightarrow F(x)=-e^{\cos x}+c\)
Mà \(F(0)=e+c=e\Rightarrow c=0\)
\(\Rightarrow F(\pi)=-e^{\cos \pi}=\frac{-1}{e}\). Đáp án B
6 tháng 3 2022
b: f(-1)=-1
f(1/2)=-1/4
c: \(f\left(1\right)=-1^2=-1=y_E\)
Do đó: E thuộc đồ thị
\(f\left(-2\right)=-\left(-2\right)^2=-4< >y_F\)
Do đó: F không thuộc đồ thị
d: Thay x=-3 vào f(x), ta được:
\(f\left(-3\right)=-\left(-3\right)^2=-9\)
12 tháng 1 2022
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
1 tháng 10 2020
ycbt\(\Leftrightarrow\hept{\begin{cases}9^4a+9^3b+9^2c+9d+e=32078\left(p\right)\\a,b,c,d,e\in N;\le8;a\ne0\end{cases}}\)
VP(p): 9 dư 2 =>e =2
\(\Rightarrow9^3a+9^2b+9c+d=\frac{32078-2}{9}=4564⋮9\Rightarrow d=0\)
\(\Rightarrow9^2a+9b+c=\frac{3564}{9}=396⋮9\Rightarrow c=0\)
\(\Rightarrow9a+b=\frac{396}{9}=44\)chia 9 dư 8 => b=8
=> 9a=36=>a=4
Vậy S =14
CM
9 tháng 3 2017
Ta có bảng biến thiên như hình vẽ sau:
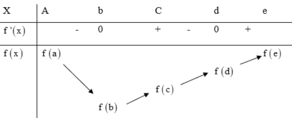
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
CM
11 tháng 4 2018
Đáp án C
Giả sử 
Hoành độ điểm D là nghiệm phương trình: 
Hoành độ điểm E là nghiệm của phương trình: 
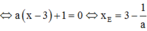
Hoành độ điểm F là nghiệm của phương trình: 
Khi đó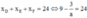 
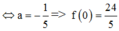
Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e