giúp mình bài này với ạ :3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: =5(x+2y)
b: =(x+y)(5x-7)
Bài 2:
a: \(=\dfrac{1+2}{xy}=\dfrac{3}{xy}\)

cot B = \(\dfrac{5}{13}=>tanB=\dfrac{13}{5}\)
AC=AB.tanB
AC= 15.\(\dfrac{13}{5}\)
AC= 39cm
BC2=AB2+AC2
BC2=225+1521=1746
BC=3 \(\sqrt{194}\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

Bài 3:
a) Ta có: \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}-\dfrac{a-4}{\sqrt{a}-2}\)
\(=\sqrt{a}+2-\left(\sqrt{a}+2\right)\)
=0
b) Ta có: \(\dfrac{9-a}{\sqrt{a}+3}-\dfrac{a-6\sqrt{a}+9}{\sqrt{a}-3}\)
\(=3-\sqrt{a}-\sqrt{a}+3\)
\(=6-2\sqrt{a}\)
c) Ta có: \(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}-\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\)
\(=\sqrt{a}-\sqrt{b}-\left(\sqrt{a}-\sqrt{b}\right)\)
=0
d) Ta có: \(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\)
\(=a+\sqrt{ab}+b+\sqrt{ab}\)
\(=a+2\sqrt{ab}+b\)
Bài 1:
a.
\(\frac{4\sqrt{5}+\sqrt{15}}{\sqrt{5}}=\frac{\sqrt{5}(4+\sqrt{3})}{\sqrt{5}}=4+\sqrt{3}\)
$\frac{7-\sqrt{7}}{3\sqrt{7}}=\frac{\sqrt{7}(\sqrt{7}-1)}{3\sqrt{7}}=\frac{\sqrt{7}-1}{3}$
\(\frac{4\sqrt{2}-\sqrt{6}}{2\sqrt{3}}=\frac{\sqrt{2}(4-\sqrt{3})}{\sqrt{2}.\sqrt{6}}=\frac{4-\sqrt{3}}{\sqrt{6}}\)
\(\frac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}=\frac{(3\sqrt{2}-2\sqrt{3})(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{6}}{3-2}=\sqrt{6}\)
b.
\(\frac{a-2\sqrt{a}}{\sqrt{a}-2}=\frac{\sqrt{a}(\sqrt{a}-2)}{\sqrt{a}-2}=\sqrt{a}\)
\(\frac{1-a\sqrt{a}}{1-\sqrt{a}}=\frac{(1-\sqrt{a})(1+\sqrt{a}+a)}{1-\sqrt{a}}=1+\sqrt{a}+a\)
\(\frac{a+10\sqrt{a}+25}{\sqrt{a}+5}=\frac{(\sqrt{a}+5)^2}{\sqrt{a}+5}=\sqrt{a}+5\)
\(\frac{a-9}{\sqrt{a}+3}=\frac{(\sqrt{a}-3)(\sqrt{a}+3)}{\sqrt{a}-3}=\sqrt{a}+3\)

Bài 1:
a: ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
b: Ta có: \(2\sqrt{3}=\sqrt{12}\)
\(3\sqrt{2}=\sqrt{18}\)
mà 12<18
nên \(2\sqrt{3}< 3\sqrt{2}\)
c: Ta có: \(\dfrac{12}{\sqrt{5}-2}=12\sqrt{5}+24\)
d: Ta có: \(\dfrac{24}{2-x}\cdot\sqrt{\dfrac{x^2-4x+4}{36}}\)
\(=\dfrac{24}{2-x}\cdot\dfrac{2-x}{6}\)
=4

a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).

Bài 3:
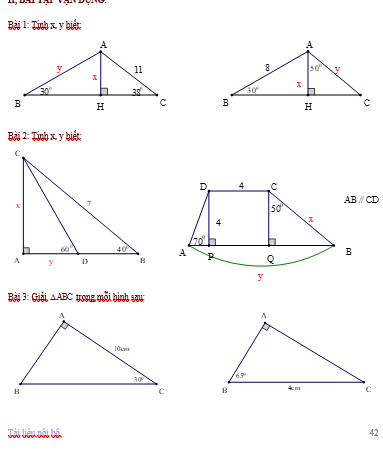
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

Bài 7 :
\(a) Na_2O + H_2O \to 2NaOH\\ SO_2 + H_2O \to H_2SO_3\\ b) Na_2O + 2HCl \to 2NaCl + H_2O\\ Fe_2O_3 + 6HCl \to 2FeCl_3 + 3H_2O\\ c) 2NaOH + SO_2 \to Na_2SO_3 + H_2O\)
Bài 8 :
a) Trích mẫu thử
Cho mẫu thử vào nước :
- mẫu thử tan là $Na_2O$
$Na_2O + H_2O \to 2NaOH$
- mẫu thử không tan là CuO
b) Trích mẫu thử
Cho giấy quỳ tím ẩm vào :
- mẫu thử hóa đỏ là $P_2O_5$
$P_2O_5 + 3H_2O \to 2H_3PO_4$
- mẫu thử hóa xanh là $Na_2O$
$Na_2O + H_2O \to 2NaOH$

\(\left(1\right)8x-3=6x+11\)
\(\Leftrightarrow2x=14\)
\(\Leftrightarrow x=7\)
Vậy ...
\(\left(2\right)7-\left(2x+4\right)=-\left(x+4\right)\)
\(\Leftrightarrow7-2x-4=-x-4\)
\(\Leftrightarrow x=7\)
Vậy ...
\(\left(3\right)\dfrac{7x-1}{6}+2x=\dfrac{16-x}{5}\)
\(\Leftrightarrow5\left(7x-1\right)+60x=6\left(16-x\right)\)
\(\Leftrightarrow35x-5+60x=96-6x\)
\(\Leftrightarrow101x=101\)
\(\Leftrightarrow x=1\)
`1)8x-3=6x+11`
`<=>8x-6x=11+3`
`<=>2x=14`
`<=>x=7`
Vậy `S = {7}`
______________________________
`2)7-(2x+4)=-(x+4)`
`<=>7-2x-4=-x-4`
`<=>2x-x=7-4+4`
`<=>x=7`
Vậy `S = {7}`
______________________________
`3)[7x-1]/6+2x=[16-x]/5`
`<=>[5(7x-1)]/30+[60x]/30=[6(16-x)]/30`
`<=>35x-5+60x=96-6x`
`<=>35x+60x+6x=96+5`
`<=>101x=101`
`<=>x=1`
Vậy `S = {1}`




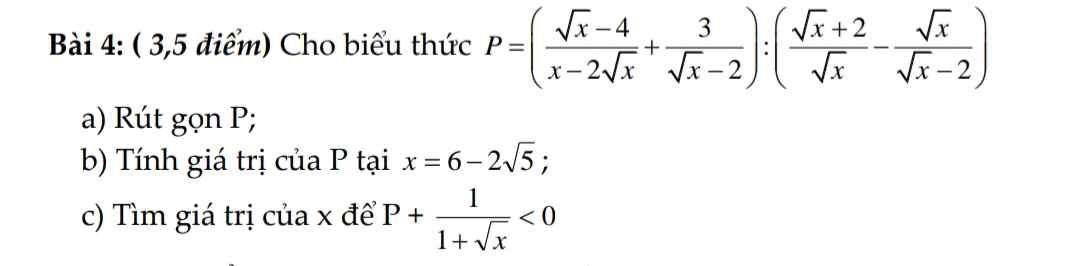



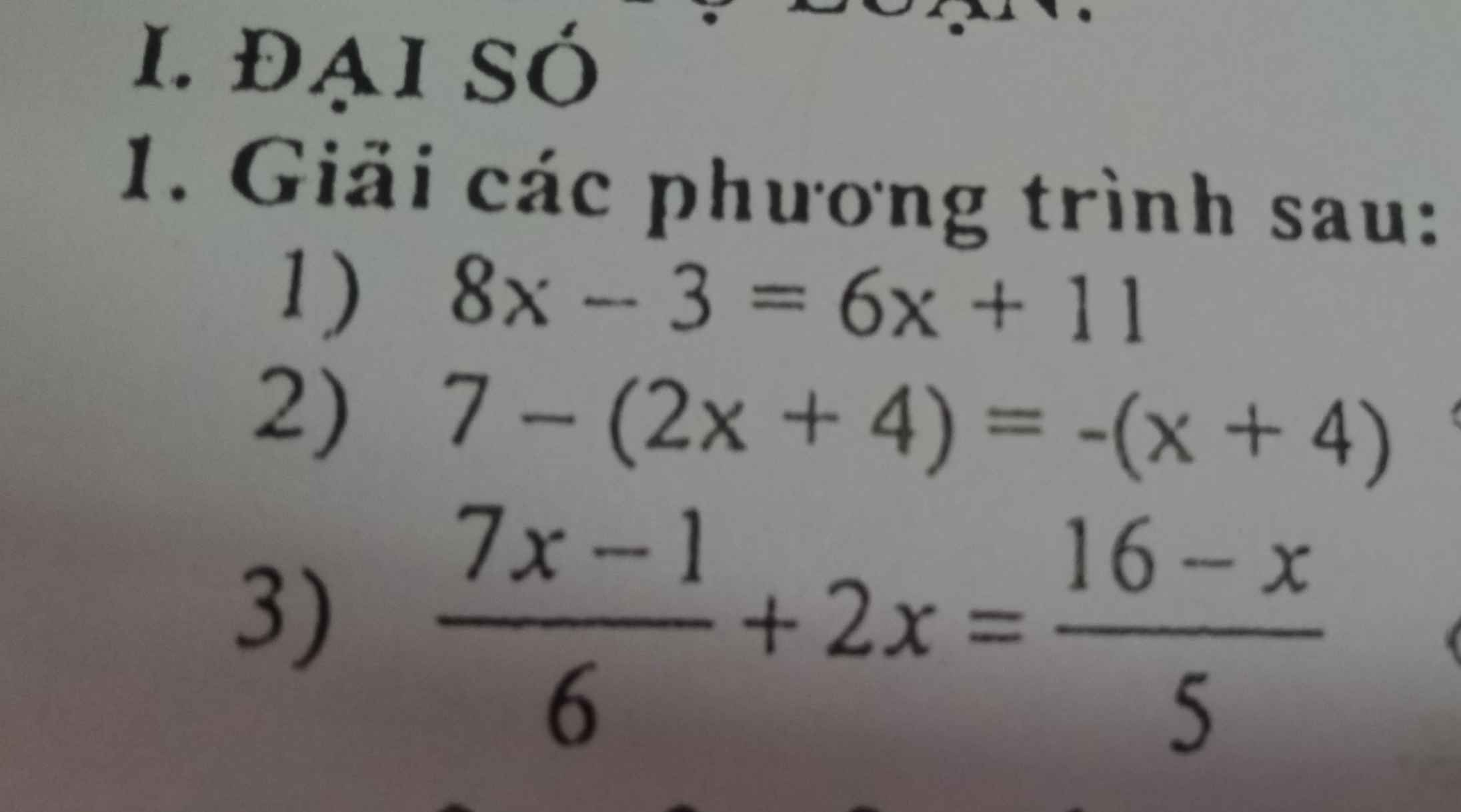
\(h=2R\)
\(V=h.\pi R^2=2R.\pi R^2=16\pi\)
\(\Rightarrow R^3=8\Rightarrow R=2\Rightarrow h=4\)
\(S_{tp}=2\pi R^2+2\pi Rh=24\pi\) \(\left(cm^2\right)\)