Giải dùm e vơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
\(\left|2x-1\right|\ge0\)
\(\Rightarrow1+\left|2x-1\right|\ge1\)
\(\Rightarrow\frac{2}{1+\left|2x-1\right|}\le\frac{2}{1}=2\)
\(\Rightarrow1+\frac{2}{1+\left|2x-1\right|}\le3\)
\(\Rightarrow B_{max}=3\)
\(\Leftrightarrow\left|2x-1\right|=0\)
\(\Leftrightarrow2x-1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy ...
Để B lớn nhất thì 2/1 + |2x - 1| lớn nhất
=> 1 + |2x - 1| nhỏ nhất
Mà 1 + |2x - 1| < hoặc = 1
Dấu" =" xảy ra khi và chỉ khi |2x - 1| = 0
=> 2x - 1 = 0
=> 2x = 1
=> x = 1/2
Vậy với x = 1/2 thì B lớn nhất = 1 + 2/1+1 = 1 + 1 = 2

\(ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow4\sqrt{2x-1}+3\sqrt{2x-1}=4\\ \Leftrightarrow\sqrt{2x-1}=\dfrac{4}{7}\\ \Leftrightarrow2x-1=\dfrac{16}{49}\\ \Leftrightarrow x=\dfrac{65}{98}\left(tm\right)\)
\(\sqrt{32x-16}+\sqrt{18x-9}=4\) (ĐKXĐ: x≥\(\dfrac{1}{2}\))
⇔ \(\sqrt{16\left(2x-1\right)}+\sqrt{9\left(2x-1\right)}=4\)
⇔ 4\(\sqrt{2x-1}\)\(+3\sqrt{2x-1}\)= 4
⇔ 7\(\sqrt{2x-1}=4\)
⇔ \(\sqrt{2x-1}=\dfrac{4}{7}\)
⇔ \(2x-1=\dfrac{16}{49}\)
⇔ 2x = \(\dfrac{65}{49}\)
⇔ x = \(\dfrac{65}{98}\) (TM)
Vậy x = \(\dfrac{65}{98}\)

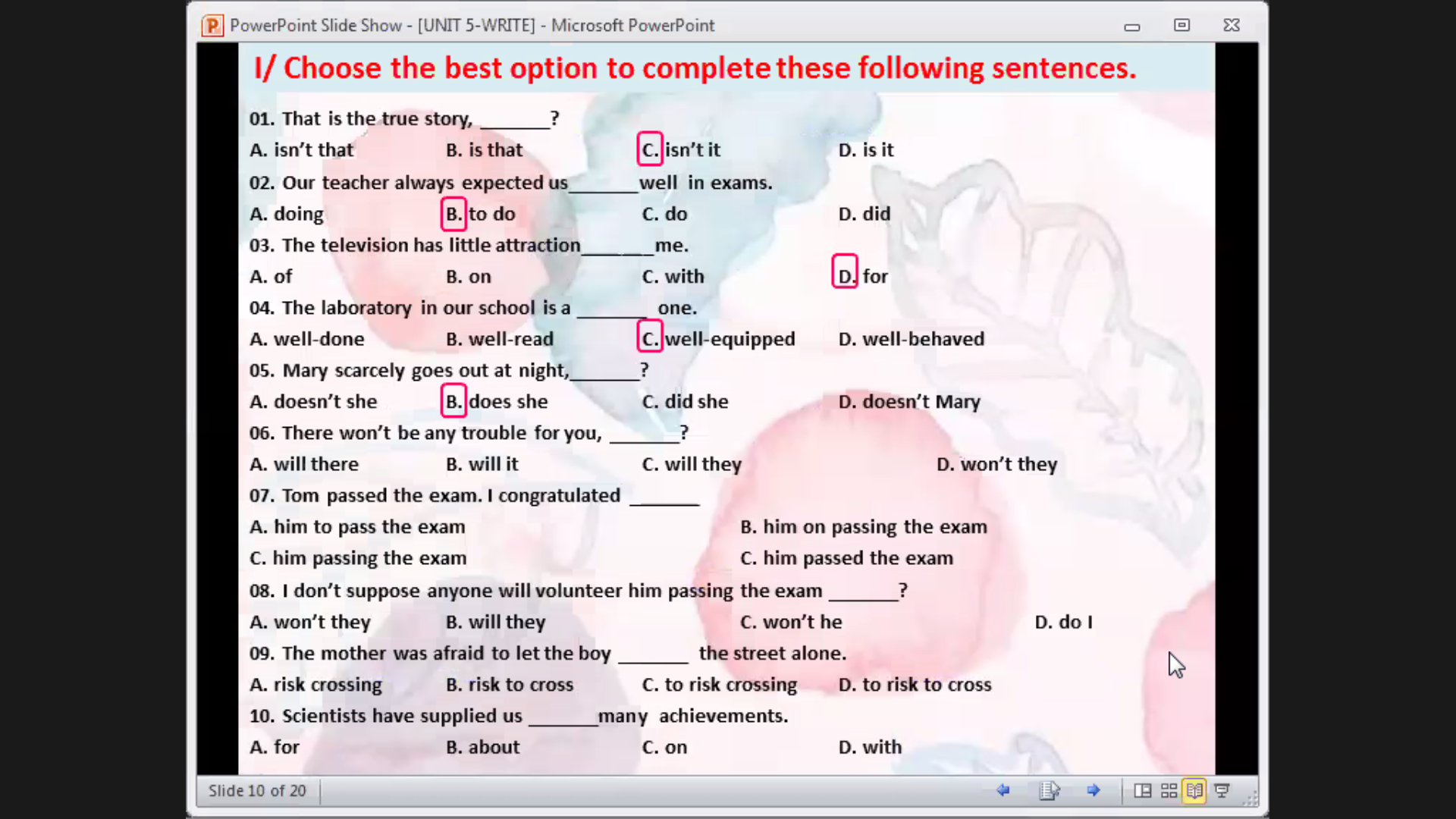
1. Chủ ngữ là "my mother" = "she" => phải dùng doesn't nha
2. "skirt" ở số ít nên phải dùng "that", "those" + danh từ số nhiều nha
3. "egg" là danh từ đếm được nên phải dùng "many", "much" dùng với danh từ không đếm được

Học sinh trung học cơ sở nên mặc quần áo bình thường
Mặc quần áo bình thường:
- làm cho học sinh cảm thấy thoải mái.
- cho học sinh tự do lựa chọn (kích cỡ, màu sắc, và kiểu dáng, v.v)
- tạo cho học sinh cảm giác tự tin khi diện những bộ quần áo yêu thích.
- làm cho trường học đầy màu sắc và sống động

\(1,\\ a,=3x\left(1-3y\right)\\ b,=9xy\left(2xy-x^2+4y\right)\\ c,=\left(x-y\right)\left(15x-5y\right)=5\left(x-y\right)\left(3x-y\right)\\ 2,\\ a,\Rightarrow2x^2\left(x^2-4\right)=0\Rightarrow2x^2\left(x-2\right)\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\\ b,\Rightarrow\dfrac{2}{5}x\left(x+10\right)-\left(x+10\right)=0\\ \Rightarrow\left(x+10\right)\left(\dfrac{2}{5}x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-10\\\dfrac{2}{5}x=1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-10\\x=\dfrac{5}{2}\end{matrix}\right.\)
\(3,\)
\(a,\left\{{}\begin{matrix}AK=KD\\BI=IC\end{matrix}\right.\Rightarrow KI\) là đtb hình thang ABCD
\(b,\) Vì KI là đtb hình thang ABCD nên \(KI=\dfrac{AB+CD}{2}=\dfrac{17}{2}=8,5\left(cm\right)\)
\(c,\) \(\left\{{}\begin{matrix}AK=KD\\KE//AB\end{matrix}\right.\Rightarrow BE=ED\Rightarrow KE\) là đtb tam giác ABD
\(\Rightarrow KE=\dfrac{1}{2}AB=2,5\left(cm\right)\)
\(\left\{{}\begin{matrix}BI=IC\\IF//AB\end{matrix}\right.\Rightarrow AF=FC\Rightarrow IF\) là đtb tam giác ABC
\(\Rightarrow IF=\dfrac{1}{2}AB=2,5\left(cm\right)\)
Ta có \(EF=KI-KE-IF=8,5-2,5-2,5=3,5\left(cm\right)\)


2.2 Đề lỗi không dịch được
2.3
\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên ta có:
\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)
Thế vào bài toán:
\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)
\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)
(Bản thân câu này đề bài cũng rất dở)







Chọn B
B