Nêu cách gải phương tình lượng giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: 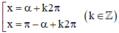
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:
ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.

- Những tình huống nguy hiểm thường xảy ra ở địa phương em và nêu cách ứng phó với tình huống:
Những tình huống nguy hiểm | Cách ứng phó với tình huống |
Lũ lụt | + Thường xuyên xem dự báo thời tiết + Tìm nơi trú ẩn an toàn + Chủ động chuẩn bị đồ phòng chống (đèn pin, thực phẩm, áo mưa…) + Gọi 112 yêu cầu cứu nạn… +…. |
Bão | + Thường xuyên xem dự báo thời tiết + Tìm nơi trú ẩn an toàn trong nhà kiến cố + Không ra ngoài,… |
*Những tình huống nguy hiểm:
-Sạt lở đất
-Ngập lụt
*Cách ứng phó:
Với sạt lở đất:-Chủ động tìm nơi chú ẩn an toàn
-Tránh xa các vùng đồi núi
-Nếu cảm thấy mình đang gặp nguy hiểm thì gọi cho xe cứu hộ
Với ngập lụt:-Chủ động tìm nơi chú ản an toàn
-Cập nhật tin tức về thời tiết
-Tránh xa các vùng có nước lớn

Tham khảo:
Những tình huống nguy hiểm | Cách ứng phó với tình huống |
Lũ lụt | + Thường xuyên xem dự báo thời tiết + Tìm nơi trú ẩn an toàn + Chủ động chuẩn bị đồ phòng chống (đèn pin, thực phẩm, áo mưa…) + Gọi 112 yêu cầu cứu nạn… +…. |
Bão | + Thường xuyên xem dự báo thời tiết + Tìm nơi trú ẩn an toàn trong nhà kiến cố + Không ra ngoài,…
|
| Tình huống nguy hiểm | Cách ứng phó |
| Sạt lở đất | -Chủ động tìm nơi chú ẩn an toàn - Tránh xa các vùng đồi núi -Nếu cảm thấy mình đang gặp nguy hiểm thì gọi cho xe cứu hộ |
| Ngập lụt | - Chủ động tìm nơi chú ản an toàn - Cập nhật tin tức về thời tiết - Tránh xa các vùng có nước lớn |

ta có thể xem cái ca đơn giản 1 chút.có nghĩa là không có quai.
ta có đường kính của 1 nguyên tử Al là 0,25 nm = 0,25.10^-6 m.
giả sử rằng cái ca chỉ cao 0,25.10^-6 m thì :
số nguyên tử Al sẽ được xếp thành vòng của cái ca.tức là chu vi của cái ca đó.
số nguyên tử Al = chu vi ca / (0,25.10^-6).
điều kiện nguyên tử Al là 1 hình tròn.
ví dụ :
l : là hằng số 0,25.10^-6.
p : chu vi ca.
h : chiều cao của ca.
n : số nguyên tử Al.
ch.cao of ca = l thì n = p/l
vậy nếu ch.cao of ca = h thì n = h.p/l^2 (cái này là nhân chéo chia ngang từ cái ở trên đó).
tất cả phải cùa đơn vị nhen.k biêt đúng hay sai nữa.

A = 1 + 2 + 22 + ........... + 29
2A = 2 + 22 + ........... + 29 + 210
2A - A = (2 + 22 + ........... + 29 + 210) - (1 + 2 + 22 + ........... + 29)
A = 210 - 1
=> A = B = 210 - 1

Lượng mưa trung bình năm của địa phương: Bằng tổng lượng mưa của nhiều năm cộng lại rồi chia cho số năm.

=>cái trên tl nhầm
Theo tác giả, cái khó trong việc tìm ra tinh thần của thơ mới là:
- Thơ cũ, thơ mới đều có bài hay, bài dở.
- Cái hôm nay phôi thai từ cái hôm qua, trong cái mới vẫn còn cái cũ rơi rớt lại.
• Tác giả đã nêu ra nguyên tắc nhận diện:
- Không căn cứ vào cục bộ và cái dở của thơ mỗi thời.
- Phải căn cứ vào đại thể và cái hay của mỗi thời.
\
copy mạng đc khum
A. Phương pháp giải & Ví dụ
- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình cosx = a (2)
♦ |a| > 1: phương trình (2) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.
Khi đó phương trình (2) có các nghiệm là
x = α + k2π, k ∈ Z
và x = -α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và cosα = a thì ta viết α = arccos a.
Khi đó các nghiệm của phương trình (2) là
x = arccosa + k2π, k ∈ Z
và x = -arccosa + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình tanx = a (3)
Điều kiện:
Nếu α thỏa mãn điều kiện và tanα = a thì ta viết α = arctan a.
Khi đó các nghiệm của phương trình (3) là
x = arctana + kπ,k ∈ Z
- Phương trình cotx = a (4)
Điều kiện: x ≠ kπ, k ∈ Z.
Nếu α thỏa mãn điều kiện và cotα = a thì ta viết α = arccot a.
Khi đó các nghiệm của phương trình (4) là
x = arccota + kπ, k ∈ Z
Ví dụ minh họa