Biết 2a2c và 2\(a^4\)\(c^2\) cùng dấu. khẳng định nào dưới đây là đúng
a)c>0
b) c<0
c) c=0
d) c khác 0
(nhớ giải thích)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì z 1 = 1 + 2 i là nghiệm phương trình z 2 + b z + c = 0 nên
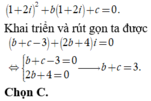

Khẳng định nào sau đây là đúng
a) (x - y)^3 = x^3 - y^3
b) x^3 +1 = (x + 1) (x^2 - x + 1)
c) (x + 2)^2 = x^2 + 4
d) x^3 - 1 = (x - 1) (x^2 + 2x + 1)
Cũng không khó đâu bạn à. Ta tháy a4 lớn hơn hoặc bằng 0; c2 lớn hơn hoặc bằng 0 => 2a4c2 lớn hơn hoặc bằng 0. Mà 2a2c và 2a4c2 cùng dấu => 2a2c lớn hơn hoặc bằng 0. Lại có a2 lớn hơn hoặc bằng 0 => 2a2c lớn hơn hoặc bằng 0 xảy ra khi và chỉ khi c lớn hơn hoặc bằng 0