Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(CT:C_{\overline{n}}H_{2\overline{n}+2}\)
\(n_{O_2}=\dfrac{36.8}{32}=1.15\left(mol\right)\)
\(\)\(C_{\overline{n}}H_{2\overline{n}+2}+\dfrac{3\overline{n}+1}{2}O_2\underrightarrow{t^0}nCO_2+\left(n+1\right)H_2O\)
\(\dfrac{2.3}{3\overline{n}+1}........1.15\)
\(M=\dfrac{10.2}{\dfrac{2.3}{3\overline{n}+1}}=\dfrac{102}{23}\left(3\overline{n}+1\right)\)
\(\Rightarrow14\overline{n}+2=\dfrac{102}{23}\cdot\left(3\overline{n}+1\right)\)
\(\Rightarrow\overline{n}=3.5\)
\(CT:C_3H_8\left(amol\right),C_4H_{10}\left(bmol\right)\)
\(m=44a+58b=10.2\left(g\right)\left(1\right)\)
\(n_{O_2}=5a+6.5b=1.15\left(2\right)\)
\(\left(1\right),\left(2\right):\)
\(a=b=0.1\)
\(\%C_3H_8=\dfrac{4.4}{10.2}\cdot100\%=43.13\%\)
\(\%C_4H_{10}=56.84\%\)

Gọi công thức chung của X, Y là CnH2n+2
\(n_{O_2}=\dfrac{36,8}{32}=1,15\left(mol\right)\)
PTHH: CnH2n+2 + \(\dfrac{3n+1}{2}\)O2 --to--> nCO2 + (n+1)H2O
\(\dfrac{2,3}{3n+1}\)<-----1,15
=> \(M_{C_nH_{2n+2}}=14n+2=\dfrac{10,2}{\dfrac{2,3}{3n+1}}\left(g/mol\right)\)
=> n = 3,5
Mà X,Y là 2 ankan kế tiếp nhau
=> X, Y là C3H8 và C4H10
Gọi số mol C3H8 và C4H10 là a, b (mol)
PTHH: C3H8 + 5O2 --to--> 3CO2 + 4H2O
a--->5a---------->3a----->4a
2C4H10 + 13O2 --to--> 8CO2 + 10H2O
b------->6,5b--------->4b------>5b
=> \(\left\{{}\begin{matrix}44a+58b=10,2\\5a+6,5b=1,15\end{matrix}\right.\)
=> a = 0,1; b = 0,1
=> \(\left\{{}\begin{matrix}m_{C_3H_8}=0,1.44=4,4\left(g\right)\\m_{C_4H_{10}}=0,1.58=5,8\left(g\right)\end{matrix}\right.\)
\(n_{CO_2}=3a+4b=0,7\left(mol\right)\)
=> \(m_{CO_2}=0,7.44=30,8\left(g\right)\)
\(m_{H_2O}=\left(4a+5b\right).18=16,2\left(g\right)\)

Gọi CTTQ của X là $C_nH_{2n+2}$
$n_X = \dfrac{1,12}{22,4} = 0,05(mol)$
$n_{O_2} = \dfrac{4,928}{22,4} = 0,22(mol)$
$C_nH_{2n+2} + \dfrac{3n+1}{2} O_2 \xrightarrow{t^o} nCO_2 + (n + 1)H_2O$
Theo PTHH : $n_{O_2} = \dfrac{3n+1}{2}n_X$
$\Rightarrow 0,22 = \dfrac{3n+1}{2}.0,05$
$\Rightarrow n = 2,6$
Vậy X gồm $C_2H_6$ và $C_3H_8$
Gọi $n_{C_2H_6} = a(mol) ; n_{C_3H_8} = b(mol)$
$C_2H_6 + \dfrac{7}{2}O_2 \xrightarrow{t^o} 2CO_2 + 3H_2O$
$C_3H_8 + 5O_2 \xrightarrow{t^o} 3CO_2 + 4H_2O$
Theo PTHH : $n_{O_2} = 3,5a + 5b = 0,22 ; n_X = a + b = 0,05$
$\Rightarrow a = 0,02 ; b = 0,03$
$\%V_{C_2H_6} = \dfrac{0,02}{0,05}.100\% = 40\%$
Đáp án B

\(n_{CO_2}=\dfrac{7,84}{22,4}=0,35\left(mol\right)\); \(n_{O_2}=\dfrac{10,64}{22,4}=0,475\left(mol\right)\)
BTKL: mCO2 + mH2O = 8,3 + 0,475.32 = 23,5 (g)
=> nH2O = \(\dfrac{23,5-0,35.44}{18}=0,45\left(mol\right)\)
=> nH = 0,9 (mol)
nC = 0,35 (mol)
=> \(n_O=\dfrac{8,3-0,35.12-0,9.1}{16}=0,2\left(mol\right)\)
Giả sử X chứa CnH2n+2Ox, Cn+1H2n+4Oy
Đặt \(\left\{{}\begin{matrix}n_{C_nH_{2n+2}O_x}=a\left(mol\right)\\n_{C_{n+1}H_{2n+4}O_y}=b\left(mol\right)\end{matrix}\right.\)
Bảo toàn C: an + bn + b = 0,35
=> 2an + 2bn + 2b = 0,7 (1)
Bảo toàn H: 2an + 2a + 2bn + 4b = 0,9 (2)
Bảo toàn O: ax + by = 0,2 (3)
(2) - (1) => 2a + 2b = 0,2 => a + b = 0,1
(1) => 2n(a+b) + 2b = 0,7
=> 0,2n + 2b = 0,7
Mà 0 < b < 0,1
=> 2,5 < n < 3,5
=> n = 3
Vậy X chứa C3H8Ox, C4H10Oy
=> \(\left\{{}\begin{matrix}a+b=0,1\\3a+4b=0,35\end{matrix}\right.\)
=> a = 0,05 (mol); b = 0,05 (mol)
Thay vào (3)
=> 0,05x + 0,05y = 0,2
=> x + y = 4
TH1: x = 1; y = 3
=> X chứa C3H8O, C4H10O3
TH2: x = 2; y = 2
=> X chứa C3H8O2, C4H10O2
TH3: x = 3; y = 1
=> X chứa C3H8O3, C4H10O

nH2O = 0,26
nCO2 = 0,28
⇒ số C trung bình trong X = nCO2 : nX
= 0,28 : 0,1 = 2,8
⇒ Trong X chứa C2H4
2 anken có phân tử khối gấp đôi nhau
⇒ Anken còn lại là C4H8
Vì hidro hóa hoàn toàn X thu được Y
chỉ gồm 2 Ankan nên Ankadien
phải có cùng số C với 1 trong 2 Anken
⇒ Ankadien đó là C4H6
( vì không có Ankadien có 2 C)
Đáp án B.

Dùng pp bảo toàn nguyên tố Oxi và bảo toàn khối lượng.
Gọi a = n(CO2) ; b = n(H2O).
Ta có: 44a + 18b = m(ankan) + m(O2) = 47 (g).
Áp dụng BT nguyên tố Oxi:
2a + b = 36,8/32 * 2 = 2,3.
Giải hệ 2 pt trên tìm được a = 0,7 ; b = 0,9.
==> m(CO2) = 30,8 (g) ; m(H2O) = 16,2 (g).

Đáp án B
nO2 đốt X = 0,46
nO2 đốt Y = 0,25
=> nO2 đốt Z = 0,46 - 0,25 = 0,21
Z no, đơn chức, mạch hở nên nCO2 = 0,21/1,5 = 0,14
Nếu X mạch hở thì nX = nZ = nNaOH = 0,07
=> Z là C2H5OH
Bảo toàn khối lượng
mX = mY + mZ - mNaOH = 7,48
Đặt a, b là số mol CO2 và H2O
=> 2a + b = 0,07 . 2 + 0,46 . 2 và 44a + 18b = 7,48 + 0,46 . 32
=> a = 0,39 và b = 0,28
=> Số C = 5,57 => C5 (0,03 mol) và C6 (0,04 mol)
Các muối gồm C2HxCOONa (0,03) và C3HyCOONa (0,04)
=> mY = 0,03(x + 91 ) + 0,04(y +103) = 7,06
=> 3x + 4y = 21 —> X = y = 3 là nghiệm duy nhất Xgồm:
C2H3COOC2H5 (0,03 mol)
C3H3COOC2H5 (0,04 mol)
=> % = 59,893%
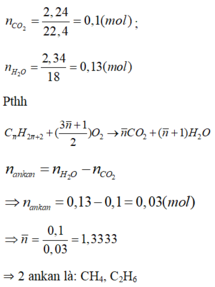


CTTQ của ankan : \(C_nH_{2n+2}\)
\(n_{O_2} = \dfrac{2,24.2}{0,082.(0+273)} = 0,2(mol)\\ C_nH_{2n+2} + \dfrac{3n+1}{2}O_2 \xrightarrow{t^o} nCO_2 + (n+1)H_2O\\ n_{ankan} = \dfrac{2}{3n+1}n_{O_2} = \dfrac{0,4}{3n+1}(mol)\\ \Rightarrow \dfrac{0,4}{3n+1}.(14n+2) = 1,76\\ \Rightarrow n = 3\)
Vậy CTPT hai ankan là : \(C_2H_6,C_4H_{10}\)