CÂU 11: Cho tứ giác ABCD, AC=BD, AC thuộc BD ; Gọi M, N ,P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó MNPQ là hình gì ? Lời giải ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
và 
. 
và 
.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
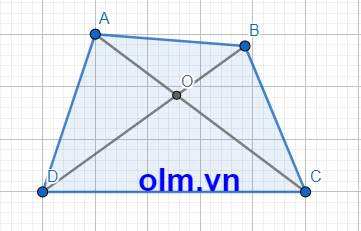
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
GV
0
CT
1
18 tháng 7 2018
tự vẽ hình nha bạn
gọi giao điểm của AC và BD la O
Ta có BO + DO = BD
mà diện h của ΔACD là: \(\frac{AC\cdot DO}{2}=\frac{8\cdot DO}{2}\)
diện h của ΔACB là: \(\frac{AC\cdot BO}{2}=\frac{8\cdot BO}{2}\)
nên diện h của tứ gái ABCD là \(\frac{8\cdot DO}{2}+\frac{8\cdot BO}{2}=\frac{8\cdot DO+8\cdot BO}{2}=\frac{8\left(DO+BO\right)}{2}=4\cdot5=20\left(cm\right)\)
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của DA
P là trung điểm của DC
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MNPQ là hbh