Ghi cách làm và đáp án giúp mình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số phần là x(x∈N*)
Ta có \(x\inƯC\left(84,105,63\right)=Ư\left(21\right)=\left\{1;3;7;21\right\}\)
Mà \(5< x< 20\Rightarrow x=7\)
Vậy chia đc 7 phần
Trong đó có 105:7=15(bút), 84:7=12(thước) và 63:7=9(vở)

Lời giải:
Giả sử có $a$ người đi tiêm vacxin. Theo bài ra thì $a\vdots 12, 10, 15$
$\Rightarrow a\vdots BCNN(12,10,15)$
$\Rightarrow a\vdots 60$
$\Rightarrow a\in\left\{0; 60; 120; 180; ....\right\}$
Vì $a$ nằm trong khoảng từ $100$ đến $130$ nên $a=120$ (người)

Bài này mình nhân chia trước cộng trừ sau:
-Rồi nếu trong phép tính có 1 thừa số là âm thì kết quả là âm (âm+dương; dương+âm)
-Còn nếu thừa số đều là "âm+âm" hay "Dương+dương" thì kết quả sẽ ra dương.
Lưu ý:Cái này chỉ áp dụng cho phép tính nhân và chia
(-3).4+(-2)(-5)-6.8
=(-12)+10-48
=(-2) - 48
=-50
Chúc bạn thi tốt nhé ^ v ^)

200 : [ 100 - ( 52. 20100 +50 ) ] + ( 72 - 6. 23 )2021
= 200 : [ 100 - ( 25 . 1 + 50 ) ] + ( 49 - 6 . 8 ) 2021
= 200 : [ 100 - ( 25 + 50 ) ] + ( 49 - 48 ) 2021
= 200 : [ 100 - 75 ] + 12021
= 200 : [ 100 - 75 ] + 1
= 200 : 25 + 1
= 8 + 1
= 9
\(200:[100-\left(5^2.2021^0+50\right)]+\left(7^2-6.2^3\right)^{2021}\)
\(200:[100-\left(25+50\right)]+\left(49-48\right)^{2021}\)
\(200:25+1\)
=8+1=9

Lời giải:
$45-3(7+x)=6$
$3(7+x)=45-6=39$
$7+x=39:3=13$
$x=13-7=6$

Cho mik lm lại nha, muốn tính 39 x 24 thì thực hiện như thế này :
39 x 24
= 39 x (20 + 4)
= 39 x 20 + 39 x 4
= 780 + 156
= 936
Chúc bạn 1 ngày thật vui nha, bn hãy tận dụng để lm bài thật tốt nhé

Ta thấy: 6 = 1 + 2 + 3
11 = 2 + 3 + 6
20 = 3 + 6 + 11
=>Từ số thứ 4 trở đi thì một số bằng tổng ba số hạng trước đó của nó.
=> Ta có các số tiếp theo:
Số thứ 8: 11 + 20 + 37 = 68
Số thứ 9: 20 + 37 + 68 = 125
Số thứ 10: 37 + 68 + 125 = 230
Vậy số thứ 8; 10 lần lượt là 125; 230

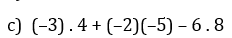
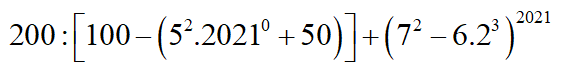
Lời giải:
$A=1+(2+2^2+2^3)+(2^4+2^5+2^6)+...+(2^{97}+2^{98}+2^{99})$
$=1+2(1+2+2^2)+2^4(1+2+2^2)+...+2^{97}(1+2+2^2)$
$=1+(1+2+2^2)(2+2^4+...+2^{97})$
$=1+7(2+2^4+...+2^{97})$ chia $7$ dư $1$
Vậy $A\not\vdots 7$