Cho hàm số y = x2 - 1. Các điểm A ( -3; 8), B ( -2; -5), C ( 1; 0), D( 1/2; 3/4 )có thuộc đồ thị của hàm số này không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


*Thay hoành độ điểm A vào phương trình hàm số :
y = 0,1. 3 2 = 0,9 = y A
Vậy điểm A(3; 0,9) thuộc đồ thị hàm số.
*Thay hoành độ điểm B vào phương trình hàm số :
y = 0,1. - 5 2 = 2,5 = y B
Vậy điểm B(-5; 2,5) thuộc đồ thị hàm số.
*Thay hoành độ điểm C vào phương trình hàm số :
y = 0,1. - 10 2 = 10 ≠ y C
Vậy điểm C(-10; 1) không thuộc đồ thị hàm số.

Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
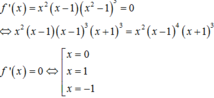
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.

Ta có
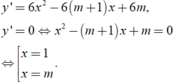
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
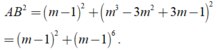
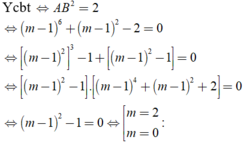
Chọn B.

Đáp án C
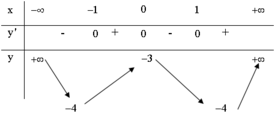
Đáp án: Hàm số y = x 2 − 2 x − 3 không có đạo hàm tại x = 0
Hàm số y = x 2 − 1 − 4 không có đạo hàm tại x = ± 1. Hàm số y = − x 4 + 2 x 2 − 3 có lim x → ± ∞ = − ∞
Nên bảng biến thiên trên không là bảng biến thiên của 3 hàm số trên. y = x 4 − 2 x 2 − 3
Kiểm tra ta có đó là bảng biến thiên của hàm số: y = x 4 − 2 x 2 − 3

Đáp án C
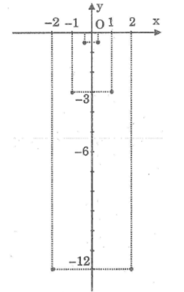
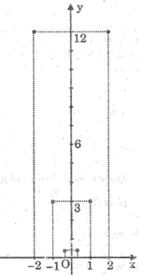
Đồ thị hàm số y = a x 2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.
Trong đồ thị các hàm số đã cho; các đồ thị nằm phía dưới trục hoành là”
(1): y = -2 x 2 ; (3): y = - 3 x 2 và (4):y = -10 x 2
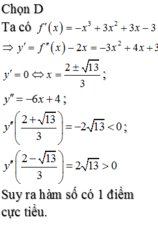


xét A, ta có:
y\(=8\)
\(y=\left(-3\right)^2-1=9-1=8\)
suy ra A(-3;8) thuộc đồ thị hàm số y=x^2-1
xét B, ta có:
y=-5
\(y=x^2-1=\left(-2\right)^2-1=4-1=3\)
suy ra B(-2;-5) ko thuộc đồ thị hàm số y=x^2-1
xét C ta có:
y=0
\(y=x^2-1=1^2-1=1-1=0\)
suy ra C(1;0) thuộc đồ thị hàm số y=x^2-1
xét D ta có:
y=3/4
\(y=x^2-1=\left(\frac{1}{2}\right)^2-1=\frac{1}{4}-1=-\frac{3}{4}\)
suy ra D(1/2;3/4) ko thuộc đồ thị hàm số y=x^2-1
vậy các điểm thuộc đồ thị hàm số y=x^2-1 là A và C