Cho tam giác ABC có AB=AC. Tia phân giác góc A cắt BC ở H ( H thuộc BC )
a, Chứng minh tam giác ABH=tam giác ACH
b, Chứng minh AH vuông góc với BC
c, Lấy điểm E thuộc cạnh AB; điểm F thuộc cạnh AC sao cho AE = AF.
Chứng minh: EF // BC
Giúp nhé mai nộp rồi ![]()

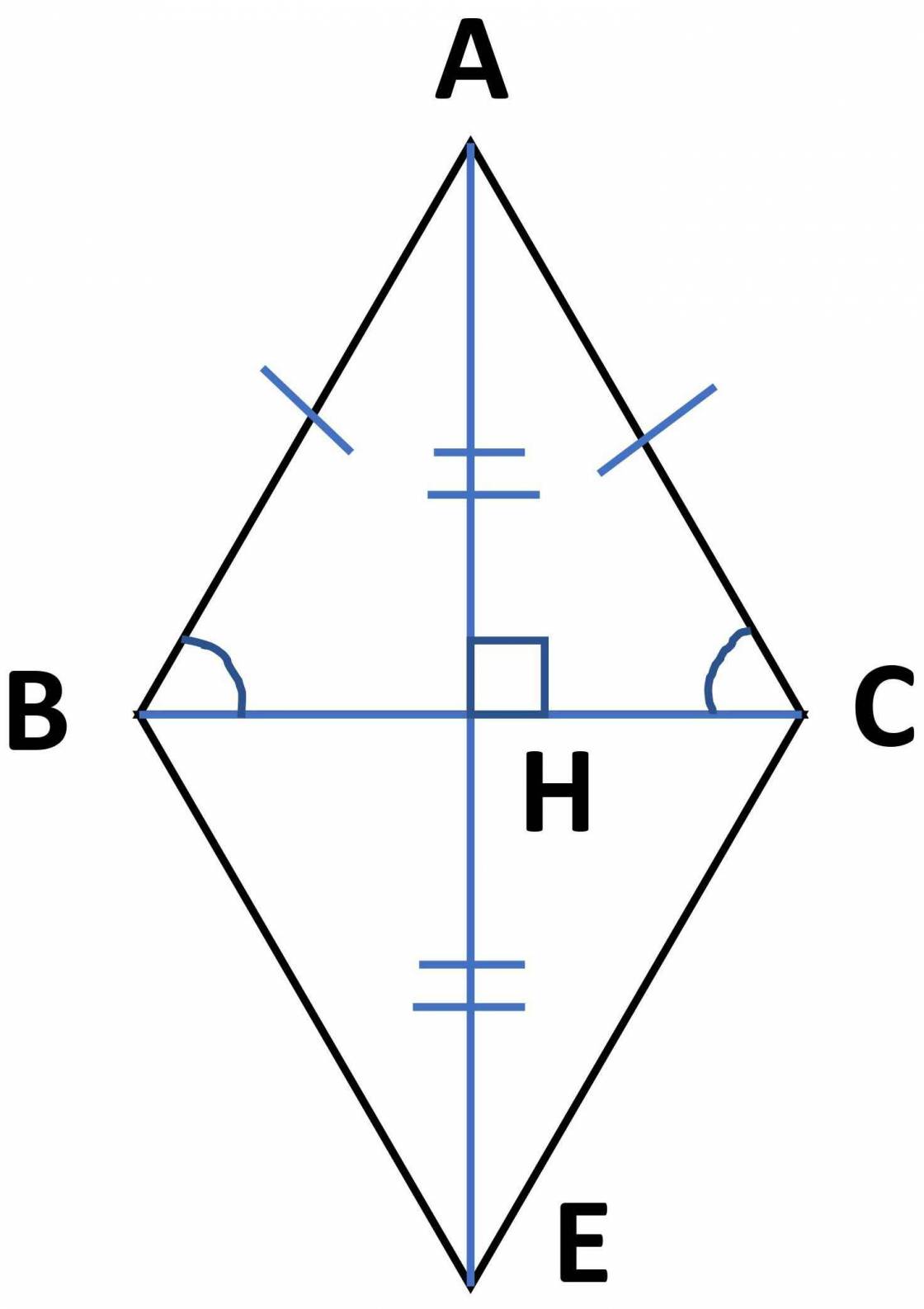
a, Xét ΔABHΔABH và ΔACHΔACH có:
AB=ACAB=AC
ˆBAH=ˆCAHBAH^=CAH^
AHAH chung
⇒ΔABH=ΔACH(c−g−c)
b, Xét ΔABCΔABC có: AB=AC
⇒ΔABC⇒ΔABC cân tại A
Xét ΔABCΔABC cân tại A có: AH là đường cao ứng với cạnh đáy BC
⇒AH⇒AH là đường cao
⇒AH⊥BC
Thank kiu nha