có cả vẽ hình và trình bày giúp mình nhé:3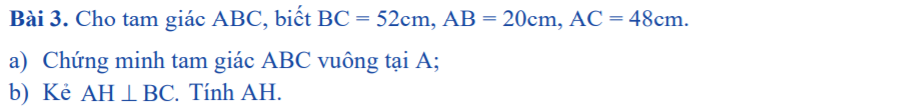
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
17 tháng 12 2021
Theo định lý Pitago ta có:
\(BC^2=AB^2+AC^2\)
=>\(17^2=8^2+AC^2\)
\(=>AC^2=225\)
=>AC=\(\sqrt{225=}15\)
Theo định lí Pitago ta có:
\(36^2+15^2=39^2\)
=>DA=39
AB+BC+CD+DA=8+17+36+39=100
GW
1
XO
31 tháng 10 2021
Nhận thấy : \(\widehat{xOy}+\widehat{OAt}=100^{\text{o}}+80^{\text{o}}=180^{\text{o}}\)
=> Oy // At
mà M \(\in Oy\)
=> OM // At
2) Xét tam giác AMB vuông tại B có
\(\widehat{MAB}+\widehat{AMB}=90^{\text{o}}\)
<=> \(\widehat{AMB}=90^{\text{o}}-\widehat{MAB}=90^{\text{o}}-50^{\text{o}}=40^{\text{o}}\)
3) \(\widehat{OMA}=\widehat{MAB}=50^{\text{o}}\left(2\text{ góc slt}\right)\)
Xét tam giác OMZ vuông tại Z
=> \(\widehat{OMZ}+\widehat{MOZ}=90^{\text{o}}\Rightarrow\widehat{MOZ}=90^{\text{o}}-\widehat{OMZ}=90^{\text{o}}-50^{\text{o}}=40^{\text{o}}=\frac{1}{2}\widehat{O}\)
=> OZ là tia phân giác của \(\widehat{O}\)
NH
1
31 tháng 8 2021
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
9 tháng 5 2017
543 + 123 = 666 ; 543 + 245 = 888 ; 543 + 234 = 777 ; 543 + 456 = 999
MT
18 tháng 9 2018
Giải :
ta đổi : 2 và 1/2m = 2 x 2 + 1 /2 = 5/2m
Cạnh tấm bìa hình vuông đó là :
5/2 : 4 = 5/2x4 = 5/8 ( m )
Diện tích tấm bìa hình vuông đó là :
5/8 x 5/8 = 5x5/8x8 = 25/64 ( m2 )
Đáp số : 25/64 m2
