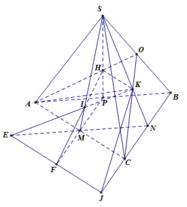
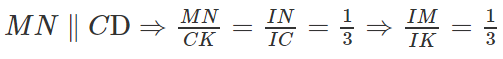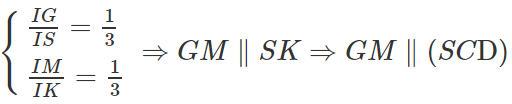Câu 1 :Cho hình chóp S.ABC , gọi M là trung điểm của BC , N là điểm thuộc cạnh AB sao cho BN = 2 NA, G là trọng tâm tam giác SBC.
1. Chứng minh NG // (SAC).
2. Xác định giao điểm I của đường thẳng MN và mặt phẳng (SAC) . Tính tỉ số \(\dfrac{IC}{CA}\).
Câu 2 :CHo hình lăng trụ ABC.A'B'C'. Trên tia đối của tia BA lấy điểm M sao cho BM=\(\dfrac{1}{2}\) BA. Gọi E là trung điểm của BC.
1. Xác định thiết diện của hình lăng trụ khi cắt bởi mặt phẳng (MEA').
2. Gọi K=BB'\(\cap\) (MEA') . Tính tỉ số \(\dfrac{BK}{BB'}\) .
Giúp mình với sắp kiểm tra rồi !!!!

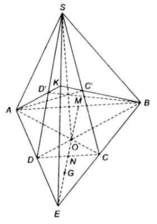
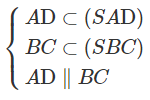
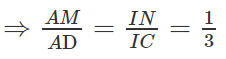
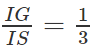
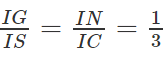 ⇒ GN // SC
⇒ GN // SC