Bài 3: (1,5 điểm) Cho hàm số có đồ thị (d) và hàm số y = có đồ thị (d’)
a) Vẽ (d) và (d’) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 12 2021
\(b,\text{PT hoành độ giao điểm: }\dfrac{1}{2}x=-x-6\\ \Leftrightarrow\dfrac{3}{2}x=6\Leftrightarrow x=4\Leftrightarrow y=2\Leftrightarrow A\left(4;2\right)\\ \text{Vậy }A\left(4;2\right)\text{ là giao điểm 2 đths}\)
31 tháng 10 2021
b, PT hoành độ giao điểm: \(2x-5=-\dfrac{1}{2}x\Leftrightarrow x=2\Leftrightarrow y=-\dfrac{1}{2}\cdot2=-1\)
\(\Leftrightarrow A\left(2;-1\right)\)
Vậy A(2;-1) là tọa độ giao điểm 2 đths
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
a.
Đồ thị xanh lá là $y=-2x+3$, xanh nước biển là $y=\frac{1}{2}x$
b. PT hoành độ giao điểm:
$y=-2x+3=\frac{1}{2}x$
$\Leftrightarrow x=\frac{6}{5}$
$y=\frac{1}{2}.\frac{6}{5}=\frac{3}{5}$
Vậy tọa độ giao điểm là $(\frac{6}{5}, \frac{3}{5})$
c.
$Gọi ptđt có dạng $y=ax+b$
Vì $A,B\in (d)$ nên:
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3=4a+b\\ 2=-a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{5}\\ b=\frac{11}{5}\end{matrix}\right.\)
Vậy ptđt là $y=\frac{1}{5}x+\frac{11}{5}$
20 tháng 12 2021
Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x-3=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
21 tháng 12 2023
c: Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Vì (d)//(d1) nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne0\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x\)+b
Thay x=4 và y=5 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot4=5\)
=>b+2=5
=>b=3
Vậy: (d): \(y=\dfrac{1}{2}x+3\)
31 tháng 8 2023
b: Phương trình hoành độ giao điểm là:
2x+1=x+3
=>2x-x=3-1
=>x=2
Thay x=2 vào y=x+3, ta được:
y=2+3=5
a: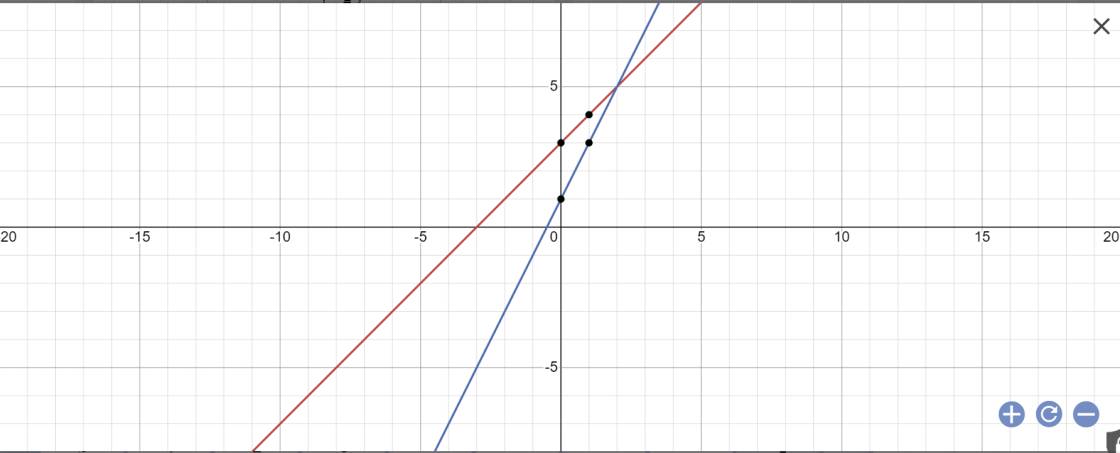 
3 tháng 9 2021
c: Vì (d2)//(d) nên \(a=-\dfrac{1}{2}\)
Thay x=-3 và y=0 vào \(y=\dfrac{-1}{2}x+b\), ta được:
\(b+\dfrac{3}{2}=0\)
hay \(b=-\dfrac{3}{2}\)
Đề thiếu rồi bạn