Tìm tất cả các giá trị tham số m để hai đồ thị hàm số \(y=-x^2-2x+3\) và \(y=x^2-m\) có điểm chung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 2 2018
Phương trình hoành độ giao điểm - x 2 - 2 x + 3 = x 2 - m
⇔ 2 x 2 + 2 x - m - 3 = 0 *
Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm
⇔ ∆ = 1 - 2 - m - 3 ≥ 0 ⇔ m ≥ - 7 2
Đáp án cần chọn là: D
CM
25 tháng 1 2018
Đáp án A
Phương trình hoành độ giao điểm
x 3 - 3 x 2 + m + 2 x - m = 2 x - 2 ⇔ x 3 - 3 x 2 + m x - m + 2 = 0 ⇔ x - 1 x 2 - 2 x - 2 + m x - 1 = 0 ⇔ x - 1 x 2 - 2 x - 2 + m = 0 ⇔ [ x = 1 g x = x 2 - 2 x - 2 + m = 0
Hai đồ thị có 3 điểm chung ⇔ g x có 2 nghiệm phân biệt khác 1
⇔ ∆ ' = 3 - m > 0 g 1 = - 3 + m ≠ 0 ⇔ m < 3
CM
11 tháng 9 2019
Đáp án C
Ta có y = x 2 x 2 − 2 x − m + x + 1 x 2 − 4 x − m − 1
Điều kiện đặt ra là mẫu có 2 nghiệm => Δ ' = 5 + m > 0 < = > m > − 5
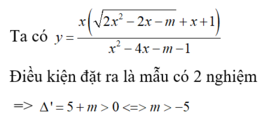
Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4