Vẽ hình và chứng minh hai góc cùng bù vs 1 góc thứ 3 thì bằng nhau
giúp mk nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)

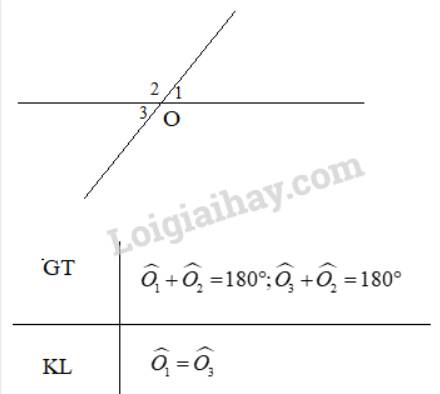
Giả sử \(\widehat {{O_1}},\widehat {{O_3}}\) cùng bù với góc \(\widehat {{O_2}}\). Ta được:
\(\widehat {{O_1}} + \widehat {{O_2}} = 180^\circ ;\widehat {{O_3}} + \widehat {{O_2}} = 180^\circ \)
\( \Rightarrow \widehat {{O_1}} =180^\circ -\widehat {{O_2}}; \widehat {{O_3}}=180^\circ -\widehat {{O_2}}\)
\( \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\) (đpcm)

| GT | \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau |
| KL | \(\widehat{CAB}=\widehat{GFE}\) |
Vì \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{CAB}=180^0\)
=>\(\widehat{CAB}=180^0-\widehat{CAD}\left(1\right)\)
Vì \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{GFE}=180^0\)
=>\(\widehat{GFE}=180^0-\widehat{CAD}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{CAB}=\widehat{GFE}\)
A C B D D
Theo bài ra ta có:\(\widehat{ACB}+\widehat{DCB}=180^o\)(hai góc bù nhau)
\(\widehat{ACB}+\widehat{ACD}=180^o\)(hai góc bù nhau)
=> \(\widehat{ACB}+\widehat{DCB}=\widehat{ACB}+\widehat{ACD}\)
=> \(\widehat{DCB}=\widehat{ACD}\)