Cho đoạn thẳng AB, O là trung điểm của AB. Vẽ hai tia Ax và By song song với nhau (Ax, By khác phía với AB). Lấy điểm M thuộc tia Ax, điểm N thược tia By sao cho AM = BN. Chứng minh ba điểm M,O,N thẳng hàng. Gợi ý: MN cắt AB tại O' rồi chứng minh O thuộc O'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 12 2023
a: Xét ΔMHA vuông tại H và ΔMKB vuông tại K có
MA=MB
\(\widehat{MAH}=\widehat{MBK}\)(hai góc so le trong, AH//BK)
Do đó: ΔMHA=ΔMKB
=>MH=MK
b: Ta có: ΔMHA=ΔMKB
=>\(\widehat{HMA}=\widehat{KMB}\)
mà \(\widehat{KMB}+\widehat{KMA}=180^0\)(hai góc kề bù)
nên \(\widehat{HMA}+\widehat{KMA}=180^0\)
=>\(\widehat{HMK}=180^0\)
=>H,M,K thẳng hàng
24 tháng 2 2020
a) +) Xét \(\Delta\)AM'B và \(\Delta\)BNA có;
^M'AB = ^NBA = 90o
AB chung
AM' = BN ( = AC)
=> \(\Delta\)AM'B = \(\Delta\)BNA
=> AN = BM'
+) Vì AM' = ABN ; AM = BN' ( = BC )
=> AM = BN'
^MAB = ^N'BA = 90o
=> \(\Delta\)AMB = \(\Delta\)BN'A
=> AN' = BM
+) Xét \(\Delta\)AMC và \(\Delta\)BCN có:
AM = BC
BN = AC
^MAC = ^CBN ( = 90o )
=> \(\Delta\)AMC = \(\Delta\)BCN
=> MC = NC
b) \(\Delta\)AM'B = \(\Delta\)BNA ( chứng minh ở a)
=> ^M'BA = ^NAB mà hai góc này ở vị trí so le trong
=> AN // BM'
\(\Delta\)AMB = \(\Delta\)BN'A
=> ^MBA = ^N'AB mà hai góc này ở vị trí so le trong
=> MB // AN'
c) Gọi O là trung điểm của AB
Xét \(\Delta\)OAM và \(\Delta\)OBN' có:
OA = OB
^OAM = ^OBN'
AM = BN'
=> \(\Delta\)OAM = \(\Delta\)OBN' => ^AOM = ^BON' mà ^AOM + ^MOB = 180o => ^BON' + ^MOB = 180o => MON' = 180o
=> M; O; N' thẳng hàng (1)
Tương tự chứng minh được:
\(\Delta\)OAM' = \(\Delta\)OBN
=> M'; O; N thẳng hàng (2)
Từ (1); (2) => MN' và M'N cắt nhau tại điểm O là trung điểm của AB
CN
30 tháng 1 2020
vào link dưới đây:
https://olm.vn/hoi-dap/detail/63073899634.html
CM
22 tháng 9 2017
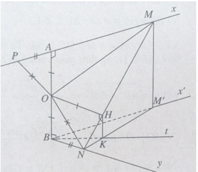
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
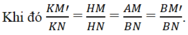
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)