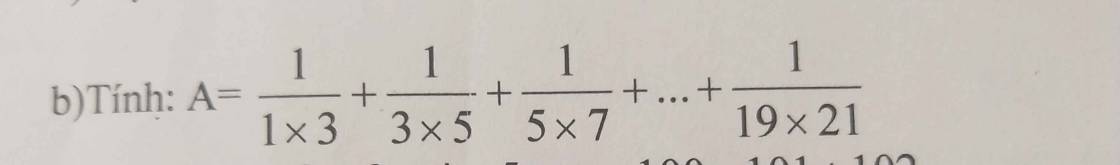ai giúp tớ với
#Hỏi cộng đồng OLM
#Toán lớp 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`#040911`
`b)`
\(A=\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{19\times21}\)
`=`\(\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{19\times21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{2}\times\dfrac{20}{21}\\ =\dfrac{10}{21}\\ \text{ Vậy, A = }\dfrac{10}{21}\)




Bài 3
a) Số học sinh tham gia môn cầu lông:
\(40\times25\%=10\) (học sinh)
b) Số học sinh tham gia môn bơi:
\(40\times15\%=6\) (học sinh)
c) Số học sinh tham gia môn Cờ vua:
\(40\times30\%=12\) (học sinh)
d) Số học sinh tham gia môn Nhảy dây:
\(40\times30\%=12\) (học sinh)
Bài 5:
a) y : 5,7 = 18,2
y : 18,2 \(\times\) 5,7
y = 103,74
b) 9,5 \(\times\) y = 23,085
y = 23,085 : 9,5
y = 2,43
Bài 6
a) Diện tích xung quanh bể:
(1,2 + 0,8) \(\times\) 2 \(\times\) 0,6 = 2,4 (m2)
Diện tích đáy bể:
1,2 \(\times\) 0,8 = 1,96 (m2)
Diện tích kính dùng làm bể:
2,4 + 1,96 = 4,36 (m2)
b) Thể tích bể:
\(1,2\times0,8\times0,6=0,576\left(m^3\right)\)

Trong toán học, định lý Pytago (còn gọi là Pythagorean theorem theo tiếng Anh) là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. Định lý có thể viết thành một phương trình liên hệ độ dài của các cạnh là a, b và c, thường gọi là "công thức Pytago":[1]
{\displaystyle a^{2}+b^{2}=c^{2},}
với c là độ dài cạnh huyền và a và b là độ dài hai cạnh góc vuông hay còn gọi là cạnh kề.
Mặc dù những hiểu biết về mối liên hệ này đã được biết trước thời của ông,[2][3] định lý được đặt tên theo nhà toán học Hy Lạp cổ đại Pythagoras (k. 570–495 BC) khi - với những tư liệu lịch sử đã ghi lại - ông được coi là người đầu tiên chứng minh được định lý này.[4][5][6] Có một số chứng cứ cho thấy các nhà toán học Babylon đã hiểu về công thức này, mặc dù có ít tư liệu cho thấy họ đã sử dụng nó trong khuôn khổ của toán học.[7][8] Các nhà toán học khu vực Lưỡng Hà, Ấn Độ và Trung Quốc cũng đều tự khám phá ra định lý này và trong một số nơi, họ đã đưa ra chứng minh cho một vài trường hợp đặc biệt.