HELP!!!!! Mình cần nộp gấp!
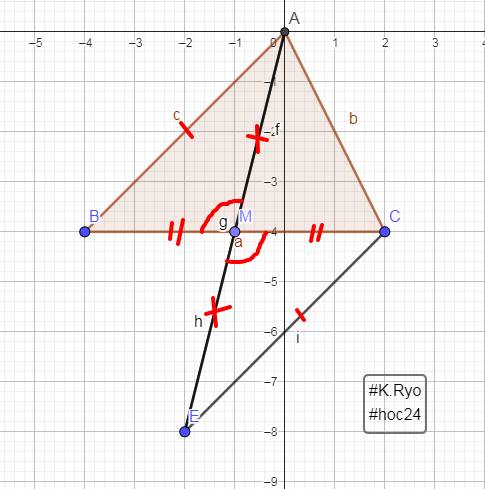
Cho tam giác A0C, M là trung điểm của 0C. Trên tia đối của MA lấy điểm E sao cho ME = MA.
a) Hai tam giác AMO và EMC bằng nhau.
b) Chứng minh rằng AO//CE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)
VT
5 tháng 12 2014
a.Xét 2 TG AMB và EMC; ta có:
MA=ME(gt); MB=MC( vì M là trung điềm BC); BMA=EMC( đối đỉnh)
=>TG AMB=TG EMC(c.g.c)
b. TG AMB= TG EMC=> BAM=MEC(2 góc tương ứng)
mà chung lại ờ vị trí slt
=>AB//CE
17 tháng 12 2016
a.Xét tam giác ABM và tam giác ECM có:
MA=ME(gt)
MB=MC(gt)
góc AMB=góc EMC(đối đỉnh)
Do đó tam giác ABM=tam giác ECM(c.g.c)
b. Vì tam giác ABM= tam giác ECM
=>góc AMB=góc CME(2 góc tương ứng)
=>AB//CE(2 góc bằng nhau ở vị trí so le trong)
Nhớ vẽ hình cho dễ so sánh nha bạn
18 tháng 2 2021
Hình thì bn tự lo nha!
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
14 tháng 9 2023
`# \text {DNamNguyenV}`
`a,`
Ta có: M là trung điểm của BC
`=> \text {MB = MC}`
Xét `\Delta ABM` và `\Delta ECM`:
`\text {MA = ME (gt)}`
\(\text{ }\widehat{\text{ AMB}}=\widehat{\text{EMC}}\left(\text{2 góc đối đỉnh}\right)\)
`\text {MB = MC}`
`=> \Delta ABM = \Delta ECM (c - g - c)`
`b,`
Vì `\Delta ABM = \Delta ECM (a)`
`=> \text {AB = CE (2 góc tương ứng)}`
18 tháng 6 2023
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔMAB=ΔMEC
b: AC>AB
=>AC>CE
c: góc BAM=góc CEA
mà góc CEA>góc CAM
nên góc BAM>góc CAM
12 tháng 11 2021
a: Xét tứ giác ACEB có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ACEB là hình bình hành
Suy ra: AC//BE
29 tháng 12 2023
a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>AB=CE
Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔHAM và ΔKEM có
HA=KE
\(\widehat{HAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔHAM=ΔKEM
=>\(\widehat{AMH}=\widehat{EMK}\)
mà \(\widehat{AMH}+\widehat{HME}=180^0\)(hai góc kề bù)
nên \(\widehat{EMK}+\widehat{HME}=180^0\)
=>H,M,E thẳng hàng
10 tháng 3 2023
a: Xét ΔAMB và ΔEMC co
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xet ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔAMD có
MH vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại M
a, xét tam giác amo và tam giác emc có
am = me ( m là trung điểm ae)
mo = mc (m là _________ oc)
góc amo = góc cme ( đối đỉnh)
=> tam giác amo bằng tam giác emc (cgc)
b, vì 2 tam giác bằng nhau cm ở câu a
=> góc aom = góc mce( cặp góc tương ứng)
mà 2 góc ở vị trí so le trong
=> oa// ce
chúc bạn học tốt, bạn có thể cho mình 1 đúng đk?
Thank you bạn! Chúc bạn 1 ngày tốt lành.