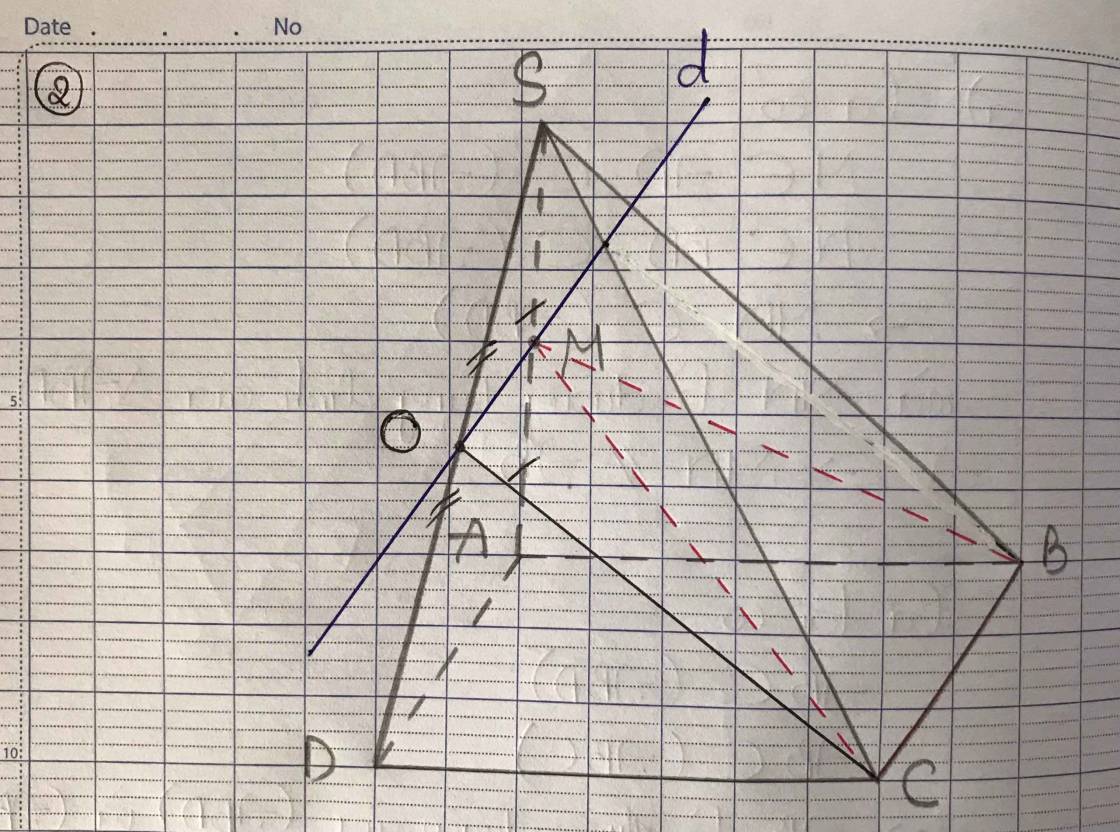
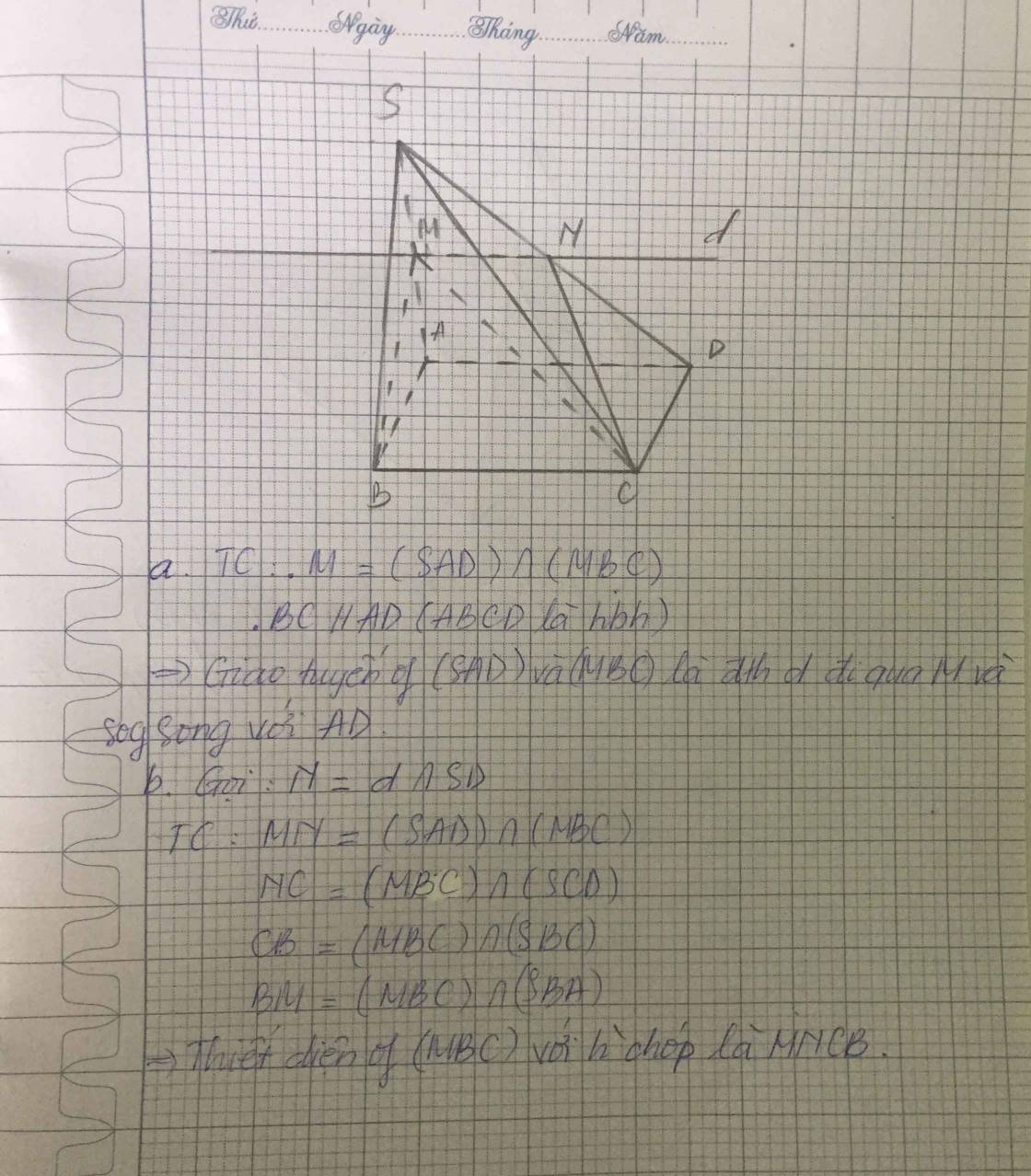
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm SA.
a. Tìm giao tuyến của (SAD) và (MBC);
b. Tìm thiết diện của mặt phẳng (MBC) với hình chóp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DQ
Dương Quốc Thanh
19 tháng 12 2021
Đúng(0)
NP
Nguyễn Phan Thanh Lịch
19 tháng 12 2021
Đúng(0)
Những câu hỏi liên quan
1 tháng 11 2023
a: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA
SA//OM
\(OM\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
b: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
29 tháng 8 2023
a/
Ta có
\(S\in\left(SAD\right);S\in\left(SBC\right)\Rightarrow S\in d\) và d//AD//BC (Nếu 2 mp lần lượt chứa 2 đường thẳng // với nhau thì giao tuyến của chúng nếu có là đường thẳng // với 2 đường thẳng đã cho)
b/
Xét tg SAD có
MA=MD; HA=HS => MH là đường trung bình của tg SAD
=> MH//SD mà \(SD\in\left(SCD\right)\) => MH//(SCD) (1)
Xét tg SAB có
HA=HS; KS=KB => MH là đường trung bình của tg SAB
=> HK//AB mà AB//CD => HK//CD mà \(CD\in\left(SCD\right)\) => HK//(SCD) (2)
Từ (1) và (2) => (MHK)//(SCD) nên không có giao tuyến
c/
Gọi O là trung điểm BD, Nối MO cắt BC tại N
Xét tg ABD có
MA=MD; OB=OD => MO là đường trung bình của tg ABD
=> MO//AB; mà HK//AB (cmt) => MO//HK
=> M; O; H; K cùng thuộc mặt phẳng MKH
\(\Rightarrow MO\in\left(MKH\right)\Rightarrow MN\in\left(MKH\right)\Rightarrow N\in\left(MKH\right)\)
Mà \(N\in BC\)
=> N là giao của BC với (MKH)
Ta có MO//HK => MN//HK => MHNK là hình thang
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
a.
Nối BN kéo dài cắt AD tại E
\(\left\{{}\begin{matrix}E\in\left(BMN\right)\\E\in\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow E=\left(BMN\right)\cap\left(SAD\right)\)
\(\left\{{}\begin{matrix}M\in SA\in\left(SAD\right)\\M\in\left(BMN\right)\end{matrix}\right.\) \(\Rightarrow M=\left(BMN\right)\cap\left(SAD\right)\)
\(\Rightarrow EM=\left(BMN\right)\cap\left(SAD\right)\)
b.
Gọi F là giao điểm EM và SD
Trong mp (SCD), nối FN kéo dài cắt SC kéo dài tại G
\(\Rightarrow G=SC\cap\left(BMN\right)\)
21 tháng 10 2023
a: Chọn mp(SBD) có chứa BM
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SO\)
Gọi E là giao điểm của SO với BM
=>E là giao điểm của BM với mp(SAC)
b: \(M\in SD\subset\left(SAD\right);M\in\left(MAC\right)\)
=>\(M\in\left(SAD\right)\cap\left(MAC\right)\)
mà \(A\in\left(MAC\right)\cap\left(SAD\right)\)
nên \(\left(MAC\right)\cap\left(SAD\right)=AM\)
27 tháng 10 2023
a: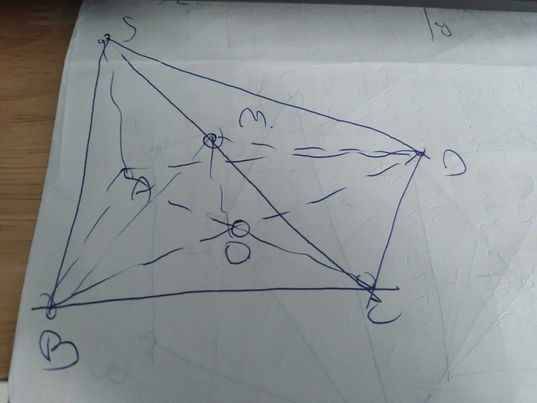 
b: \(O\in AC\subset\left(SAC\right);M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔCAS có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình
=>OM//SA và OM=SA/2
OM//SA
\(SA\subset\left(SAD\right)\)
OM không nằm trong mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không nằm trong mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
OM//SA
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA