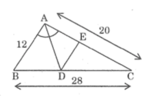
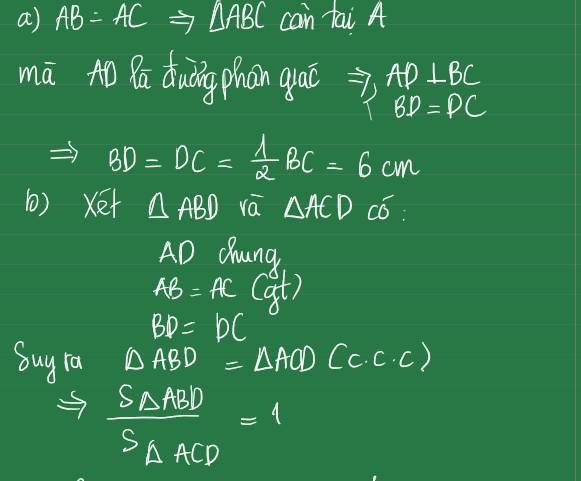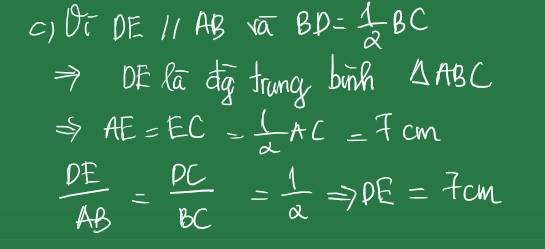cho tam giác ABC biết AB=14cm AC=35cm đường phân giác AD bằng 12cm diện tích tam giác ABC là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
3
8 tháng 3 2016
Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)
QH
17 tháng 3 2015
Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)
LN
2
25 tháng 3 2018
vẽ: DE//AB, ta có: \(\frac{AE}{EC}=\frac{DB}{BC}=\frac{AB}{AC}\)
thay vào AE/EC ta có: \(\frac{AE}{EC}=\frac{14}{35}\)
đặt AE = x thì EC = 35 - x, thay vao đăng thức, ta có:
\(\frac{x}{35-x}=\frac{14}{35}\)
\(\Rightarrow490-14x=35x\)
\(\Rightarrow x=10\)
trong tam giác AED cân tại E vẽ đường cao EH.
=> EH là đường trung tuyến nên AH = 6.
áp dụng ĐL pi-ta-go vào tam giác vuông AHE.
\(\Rightarrow EH=8\text{ nen }S_{\text{tam giác }}ADE=48cm^2\)
do tam giác ADE và DCE có chung đường cao nên SDEC = 120 cm2
\(\Rightarrow\orbr{\begin{cases}S_{ADC}=168cm^2\\S_{ABC}=235,2cm^2\end{cases}}\)
CM
27 tháng 8 2018
Vì △ ABD và △ ABC có chung đường cao kẻ từ đỉnh A nên:
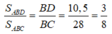
Vậy: S A B D = 3/8.S
S A D C = S A B C - S A B D = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: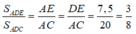 
Vậy: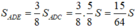 
Ta có: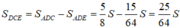 
UT
13 tháng 3 2021
a) Xét ΔHBAΔHBA và ΔABCΔABC có:
ˆAHB=ˆCAB=90∘AHB^=CAB^=90∘
ˆBB^ là góc chung
⇒ΔHBA∼ΔABC⇒ΔHBA∼ΔABC (g-g)
c) ΔABCΔABC có ADAD là đường phân giác, theo tính chất đường phân giác ta có:
⇒ABAC=DBDC=1216=34⇒ABAC=DBDC=1216=34
SΔABD=12⋅AH⋅BDSΔABD=12·AH·BD
SΔACD=12⋅AH⋅DCSΔACD=12·AH·DC
⇒SΔABDSΔACD=BDDC=34⇒SΔABDSΔACD=BDDC=34
