Question

[Nguyễn Minh Đoàn]

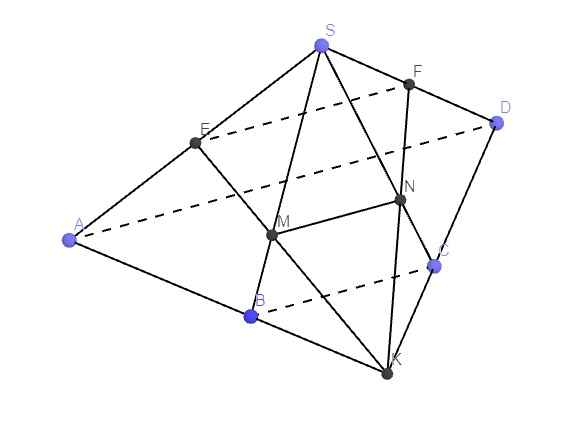
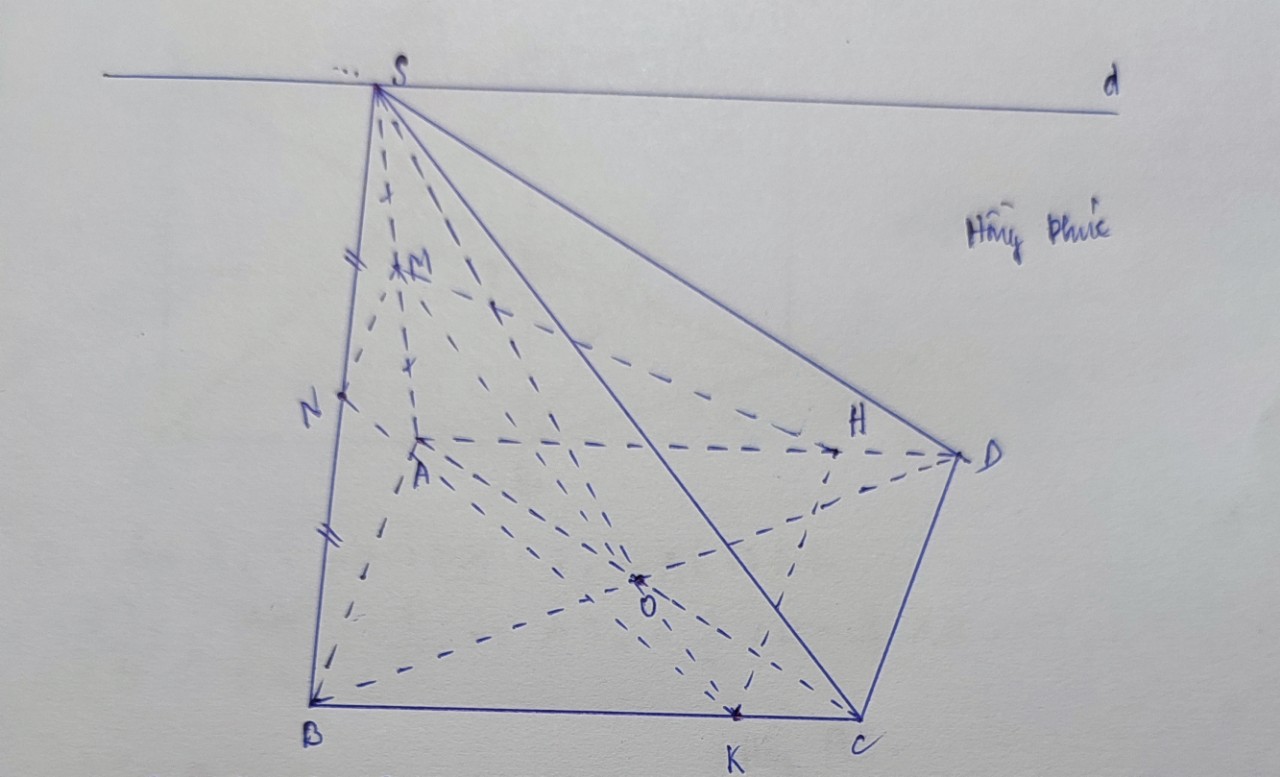
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB = 2CD.Gọi M,N lần lượt là trung điểm của các cạnh bên SA,SB và O là giao điểm của AC và BD .

a) Tìm giao tuyến của (SAC) và (SBD),(SAD) và (SBC) .

b) Chứng minh:MN // CD và MD // NC

c) Tìm giao điểm của đường thẳng AN với (SCD)

d)Gọi I trên SC sao cho SI = 2IC. C/m:SA // (IBD)

e) Gọi G là trọng tâm SBC. C/m:OG // (SCD) .

Answer 1

[Hồng Phúc]

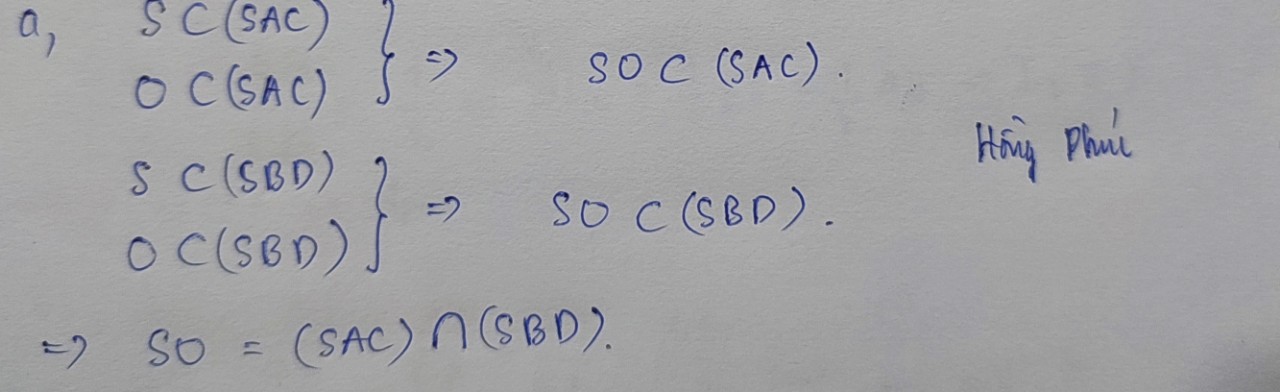
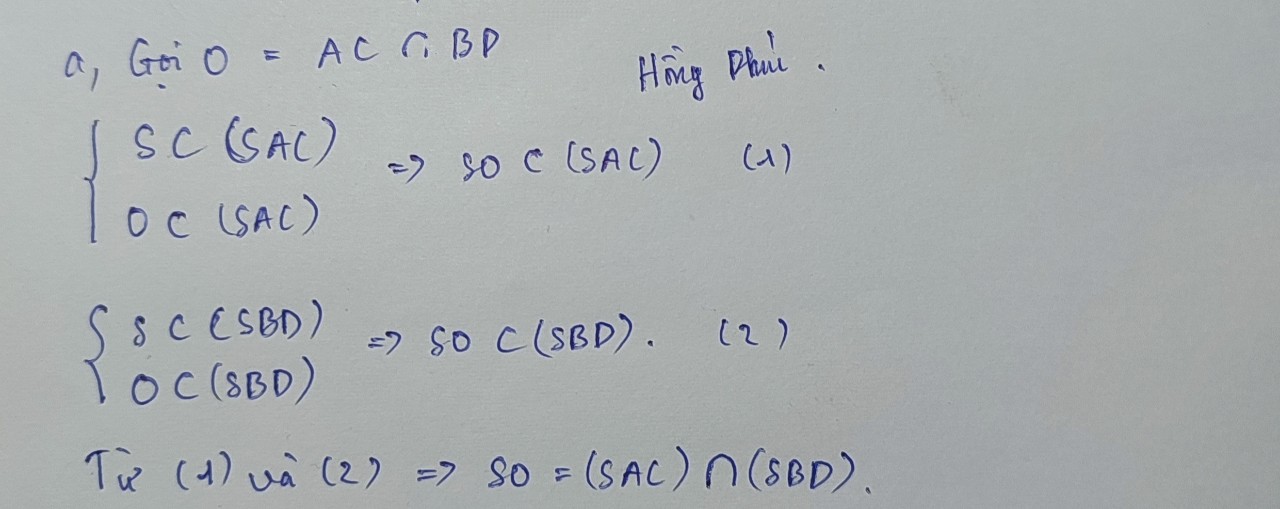
a, \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\O\subset\left(SAC\right)\end{matrix}\right.\Rightarrow SO\subset\left(SAC\right)\)

\(\left\{{}\begin{matrix}S\subset\left(SBD\right)\\O\subset\left(SBD\right)\end{matrix}\right.\Rightarrow SO\subset\left(SBD\right)\)

\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)

Gọi \(K=AD\cap BC\)

\(\Rightarrow\left\{{}\begin{matrix}S\subset\left(SAD\right)\\K\subset\left(SAD\right)\end{matrix}\right.\Rightarrow SK\subset\left(SAD\right)\)

\(\left\{{}\begin{matrix}S\subset\left(SBC\right)\\K\subset\left(SBC\right)\end{matrix}\right.\Rightarrow SK\subset\left(SBC\right)\)

\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)

Answer 2

[Hồng Phúc]

b, \(MN\) là đường trung bình.

\(\Rightarrow MN//AB\)

Lại có: \(CD//AB\)

\(\Rightarrow MN//CD\)

Mặt khác: \(MD=\dfrac{1}{2}AB=CD\Rightarrow MNCD\) là hình bình hành.

\(\Rightarrow MD//NC\)