Mạch dao động có L=20.10-6H, R=2 ôm, C=2000pF. Cần phải cung cấp cho mạch 1 công suất là bnhiu để duy trì dao động trong mạch, biết hiệu điện thế cực đại giữa 2 bản tụ là 5V.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
O
ongtho
Giáo viên
24 tháng 1 2015
Để duy trì dao động của mạch thì ta cần cung cấp cho mạch một năng lượng có công suất bằng công suất tỏa nhiệt trên điện trở.
Ta có: \(\frac{1}{2}CU_0^2=\frac{1}{2}LI_0^2\Rightarrow I_0=U_0\sqrt{\frac{C}{L}}\)
\(\Rightarrow I_0=5.10^{-2}\)(A)
\(\Rightarrow I=\frac{I_0}{\sqrt{2}}=\frac{5}{\sqrt{2}}.10^{-2}\)(A)
Công suất tỏa nhiệt trên điện trở: \(P=I^2R=\left(\frac{5}{\sqrt{2}}.10^{-2}\right)^2.2=2,5.10^{-3}J\)
Vậy công suất cần cung cấp là \(2,5.10^{-3}J\)
HY
22 tháng 1 2015
Mạch dao động có cuộn cảm L có điện trở R => năng lượng sẽ bị hao phí do tỏa nhiệt trên R.
Công suất hao phí trên điện trở R là \(P = I^2R = \frac{U^2}{R} = \frac{U_0^2}{2R} = \frac{5^2}{2.2} = 6,25W.\)
=> Cần cung cấp cho mạch 1 công suất chính bằng công suất hao phí là 6,25 W.
VT
24 tháng 5 2018
Đáp án D
+ Dòng điện cực đại trong mạch
I 0 = C L U 0 = 0 , 2 . 10 - 6 2 . 10 - 3 12 = 0 , 12 A
Công suất cung cấp cho mạch bằng công suất tỏa nhiệt trên điện trở
P = 0 , 5 I 0 2 R = 0 , 5 . 0 , 12 2 . 0 , 01 = 72 . 10 - 6 W
VT
15 tháng 3 2018
Dòng điện cực đại trong mạch
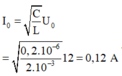
→ Công suất cung cấp cho mạch bằng công suất tỏa nhiệt trên điện trở
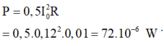
Đáp án D
VT
14 tháng 10 2018
Chọn B.
Khi hiệu điện thế cực đại trên tụ là 5V thì cường độ dòng điện hiệu dụng trong mạch là 
= 0,035355A.
Công suất tiêu thụ trong mạch là
P = RI2 = 1,25.10-4W = 0,125mW.
Muốn duy trì dao động trong mạch thì cứ sau mỗi chu kì dao động ta phải cung cấp một phần năng lượng bằng phần năng lượng đã bị mất tức là ta phải cung cấp một công suất đúng bằng 0,125mW.
VT
17 tháng 9 2018
Đáp án B
Phương pháp: Áp dụng công thức tính công suất và công thức tính năng lượng mạch dao động
Cách giải: Nếu mạch dao động luôn có U0= 12V thì về mặt năng lượng ta có:
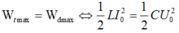
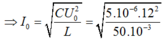
\(U_{C\left(max\right)}\Rightarrow I_{max}\) => trong mạch xảy ra cộng hưởng \(\Rightarrow Z_L=Z_C\)
\(\Rightarrow\omega L=\dfrac{1}{\omega C}\Rightarrow\omega=\dfrac{1}{\sqrt{LC}}\)
\(I_0=\omega.C.U_0=\dfrac{1}{\sqrt{LC}}.C.U_0=U_0.\sqrt{\dfrac{C}{L}}=5.\sqrt{\dfrac{2000.10^{-12}}{20.10^{-6}}}=0,05\left(A\right)\)
\(\Rightarrow P=\dfrac{I_0^2.R}{2}=\dfrac{0,05^2.2}{2}=2,5.10^{-3}\left(W\right)\)
Giúp :)