Bài 2: Tìm x, biết
a) | b) |
c) | d) |
e) (x – | g) 5x + 5 x + 2 = 650 |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, x - 3 : 2 = 5 14 : 5 12
=> x - 3 : 2 = 5 2
=> x - 3 : 2 = 25
=> x – 3 = 25
=> x = 53
b, 30 : x - 7 = 15 19 : 15 18
=> 30 : x - 7 = 15
=> x – 7 = 2
=> x = 9
c, x 70 = x
=> x 70 - x = 0
=> x ( x 69 - 1 ) = 0
=> 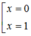
d, 2 x + 1 3 = 9 . 81
=> 2 x + 1 3 = 9 3
=> 2x + 1 = 9
=> x = 4
e, 5 x + 5 x + 2 = 650
=> 5 x 1 + 5 2 = 650
=> 5 x . 26 = 650
=> 5 x = 25
=> x = 2
f, 4 x - 1 2 = 25 . 9
=> 4 x - 1 2 = 5 2 . 3 2
=> 4 x - 1 2 = 15 2
=> 4x – 1 = 15
=> x = 4

Bài 10:
a) (x+2)2 -x(x+3) + 5x = -20
=> x2 + 4x + 4 - x2 - 3x + 5x = -20
=> 6x = -20 + (-4)
=> 6x = -24
=> x = -4
b) 5x3-10x2+5x=0
=>5x(x2-2x+1)=0
=>5x(x-1)2 =0
=> 5x=0 hoặc (x-1)2=0
=>x=0 hoặc x=1
c) (x2 - 1)3 - (x4 + x2 + 1)(x2 - 1) = 0
=> (x2 - 1)[(x2 - 1)2 - (x4 + x2 + 1)] = 0
<=> (x2 - 1)(x4 - 2x2 + 1 - x4 - x2 - 1) = 0
<=> (x2 - 1)(-3x2) = 0
<=> (x2 - 1)=0 hoặc (-3x2) =0
<=> x2=1 hoặc x2=0
<=> x=−1;1 hoặc x=0
d)
(x+1)3−(x−1)3−6(x−1)2=-19
⇔x3+3x2+3x+1−(x3−3x2+3x−1)−6(x2−2x+1)+19=0
⇔x3+3x2+3x+1−x3+3x2−3x+1−6x2+12x−6+19=0
⇔12x+13=0⇔12x+13=0
⇔12x=-13
⇔x=-23/12
Học tốt nhé:333![]()

a) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-3\right)\left(5x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
c) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
d) \(\Rightarrow\left(x-7\right)\left(3x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(a,\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\\ c,\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\\ d,\Leftrightarrow\left(x-7\right)\left(3x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)

Lời giải:
a. $2x^2+3(x-1)(x+1)=5x(x+1)$
$\Leftrightarrow 2x^2+3x^2-3=5x^2+5x$
$\Leftrightarrow 5x^2-3=5x^2+5x$
$\Leftrightarrow 5x=-3$
$\Leftrightarrow x=\frac{-3}{5}$
b.
PT $\Leftrightarrow (-5x^2-2x+16)+4(x^2-x-2)=4-x^2$
$\Leftrightarrow -x^2-6x+8=4-x^2$
$\Leftrightarrow -6x+8=4$
$\Leftrightarrow -6x=-4$
$\Leftrightarrow x=\frac{2}{3}$
c.
PT $\Leftrightarrow 4(x^2+4x-5)-(x^2+7x+10)=3(x^2+x-2)$
$\Leftrightarrow 4x^2+16x-20-x^2-7x-10=3x^2+3x-6$
$\Leftrightarrow 3x^2+9x-30=3x^2+3x-6$
$\Leftrightarrow 6x=24$
$\Leftrightarrow x=4$

1.
\(G=\dfrac{2}{x^2+8}\le\dfrac{2}{8}=\dfrac{1}{4}\)
\(G_{max}=\dfrac{1}{4}\) khi \(x=0\)
\(H=\dfrac{-3}{x^2-5x+1}\) biểu thức này ko có min max
2.
\(D=\dfrac{2x^2-16x+41}{x^2-8x+22}=\dfrac{2\left(x^2-8x+22\right)-3}{x^2-8x+22}=2-\dfrac{3}{\left(x-4\right)^2+6}\ge2-\dfrac{3}{6}=\dfrac{3}{2}\)
\(D_{min}=\dfrac{3}{2}\) khi \(x=4\)
\(E=\dfrac{4x^4-x^2-1}{\left(x^2+1\right)^2}=\dfrac{-\left(x^4+2x^2+1\right)+5x^4+x^2}{\left(x^2+1\right)^2}=-1+\dfrac{5x^4+x^2}{\left(x^2+1\right)^2}\ge-1\)
\(E_{min}=-1\) khi \(x=0\)
\(G=\dfrac{3\left(x^2-4x+5\right)-5}{x^2-4x+5}=3-\dfrac{5}{\left(x-2\right)^2+1}\ge3-\dfrac{5}{1}=-2\)
\(G_{min}=-2\) khi \(x=2\)