Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


một nửa học toán=1/2 học toán
Phần học sinh còn lại chiếm: \(1-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{7}\right)=\frac{3}{28}\)
Ngài có số học sinh là: \(3:\frac{3}{28}=3\cdot\frac{28}{3}=28\)(học sinh)
Chúc bạn học tốt!^_^

Tam giác ABC vuông tại C nên
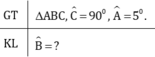
Áp dụng định lý tổng ba góc trong một tam giác ta có:
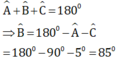

549 + X = 1326
X = 1326 - 549
X = 777
X - 636 = 5618
X = 5618 + 636
X = 6254
Giả thiết:
- Thời gian trong mưa bằng nhau.
- Bỏ qua tác động của gió nên mưa rơi thẳng đứng;
- Trong cùng một diện tích có lượng mưa như nhau. Chạy có vận tốc lớn hơn đi bộ vì vậy sẽ đón được hạt mưa nhiều hơn dẫn đến dính mưa nhiều hơn
Tuy nhiên cũng có 1 khả năng khác là"
Chạy hay đi bộ đều dính nước mưa như nhau. Vì khi ta di chuyển theo phương ngang và giả sử mưa theo phương thẳng đứng thì trên hệ quy chiếu quán tính là ta thì nước mưa rơi theo góc nghiêng (a) với mặt đất với tan(a) = V/v (V: Vân tốc hạt mưa với đất, v: Vận tốc người với đất) . Và người đi càng nhanh thì góc (a) càng nhỏ nghĩa là mưa tấp càng trực diện người hơn và càng nhanh bị ướt hơn. Nên dù đi nhanh (ướt nhanh nhưng thời gian di chuyển ngắn) hay chậm (ướt chậm nhưng thời gian di chuyển dài) thì vẫn bị ướt như nhau.
4. Đố: Tháp nghiêng Pi-da ở I-ta-li-a nghiêng 50 so với phương thẳng đứng . Tính số đo của góc ABC .

Ta có: tam giác nghiêng 50 tại A và tam giác ABC là tam giác vuông, vuông ở C. Nên ∠A + ∠B = 900
⇔ 50+ ∠B = 900
⇒ ∠B = 900 – 50 = 850
Vậy số đo góc ABC là: ∠A =50;∠B = 850;∠C= 900

a) Vì \(\frac{\pi }{2} < a < \pi \) nên \(\cos a < 0\). Do đó \(\cos a = \sqrt {1 - {{\sin }^2}a} = \sqrt {1 - \frac{1}{3}} = - \frac{{\sqrt 6 }}{3}\)
Ta có: \(\cos \left( {a + \frac{\pi }{6}} \right) = \cos a\cos \frac{\pi }{6} - \sin a\sin \frac{\pi }{6} = - \frac{{\sqrt 6 }}{3}.\frac{{\sqrt 3 }}{2} - \frac{1}{{\sqrt 3 }}.\frac{1}{2} = - \frac{{\sqrt 3 + 3\sqrt 2 }}{6}\)
b) Vì \(\pi < a < \frac{{3\pi }}{2}\) nên \(\sin a < 0\). Do đó \(\sin a = \sqrt {1 - {{\cos }^2}a} = \sqrt {1 - \frac{1}{9}} = - \frac{{2\sqrt 2 }}{3}\)
Suy ra \(\tan a\; = \frac{{\sin a}}{{\cos a}} = \frac{{ - \frac{{2\sqrt 2 }}{3}}}{{ - \frac{1}{3}}} = 2\sqrt 2 \)
Ta có: \(\tan \left( {a - \frac{\pi }{4}} \right) = \frac{{\tan a - \tan \frac{\pi }{4}}}{{1 + \tan a\tan \frac{\pi }{4}}} = \frac{{\frac{{\sin a}}{{\cos a}} - 1}}{{1 + \frac{{\sin a}}{{\cos a}}}} = \frac{{2\sqrt 2 - 1}}{{1 + 2\sqrt 2 }} = \frac{{9 - 4\sqrt 2 }}{7}\)

\(\dfrac{\Omega}{2}< a< \Omega\)
=>\(cosa< 0\)
\(sin\alpha=\dfrac{1}{3}\)
\(\Leftrightarrow cos^2\alpha=1-sin^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
mà cosa<0
nên \(cos\alpha=-\dfrac{2\sqrt{2}}{3}\)
\(cos\left(\alpha-\dfrac{\Omega}{6}\right)=cos\alpha\cdot cos\left(\dfrac{\Omega}{6}\right)+sin\alpha\cdot sin\left(\dfrac{\Omega}{6}\right)\)
\(=-\dfrac{2\sqrt{2}}{3}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{3}\cdot\dfrac{1}{2}\)
\(=\dfrac{-2\sqrt{6}+1}{6}\)

\(\cos \alpha = - \sqrt {1 - {{\left( { - \frac{5}{{13}}} \right)}^2}} = - \frac{{12}}{{13}}\) (vì \(\pi < \alpha < \frac{{3\pi }}{2}\))
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \sin \alpha \cos \frac{\pi }{6} + \cos \alpha sin\frac{\pi }{6} = \frac{{ - 12 + 5\sqrt 3 }}{{26}}\)
\(\cos \left( {\frac{\pi }{4} - \alpha } \right) = \cos \frac{\pi }{4}\cos \alpha + \sin \frac{\pi }{4}sin\alpha = \frac{{ - 17\sqrt 2 }}{{26}}\)

a/ \(\pi< x< \frac{3\pi}{2}\Rightarrow sinx< 0\)
\(\Rightarrow sinx=-\sqrt{1-cos^2x}=-\frac{5}{13}\)
\(sin\left(\frac{\pi}{3}-x\right)=sin\frac{\pi}{3}cosx-cos\frac{\pi}{3}sinx=\frac{\sqrt{3}}{2}.\left(-\frac{12}{13}\right)-\frac{1}{2}.\left(-\frac{5}{13}\right)=\frac{5-12\sqrt{3}}{26}\)
b/ \(\pi< x< \frac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\frac{3}{5}\)
\(cot\left(x-\frac{\pi}{4}\right)=\frac{cos\left(x-\frac{\pi}{4}\right)}{sin\left(x-\frac{\pi}{4}\right)}=\frac{sinx+cosx}{sinx-cosx}=7\)
c/ \(cot\left(\frac{5\pi}{2}-x\right)=cot\left(2\pi+\frac{\pi}{2}-x\right)=tanx=2\)
\(\Rightarrow tan\left(x+\frac{\pi}{4}\right)=\frac{tanx+tan\frac{\pi}{4}}{1-tanx.tan\frac{\pi}{4}}=\frac{2+1}{1-2.1}=-3\)

Bạn ấn vào biểu tượng fx để nhập công thức nhé, nhìn thế này khó luận lắm.
Một vật khối lượng 300g thực hiện đồng thời hai dao động là x1= \(5\sqrt{3}\) cos(5\(\pi\) t) cm ; x2= 5 cos (5\(\pi\) t -\(\alpha\)) cm. Biết phương trình dao động tổng hợp của vật x= A cos (5\(\pi\)t - \(\beta\)) cm. Biết 0<\(\beta\)<\(\alpha\)<\(\pi\), \(\alpha\)+\(\beta\)=\(\pi\)/2 . Năng lượng dao động của vật là
Giúp mình với nha.Mình đang cần gấp. Cảm ơn trước nhé.

Pi=3,14
Pi còn là tỉ lệ vàng(xem trên tv chỉ ngớ đc bằng đó)