Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
mặc định mảnh nhỏ là m1 còn mảnh to là m2 nhé
a) Áp dụng định lý hàm cos:
\(p_2^2=p_1^2+p^2-2p_1p\cos\left(p_1;p\right)\)
\(\Rightarrow p_2=\sqrt{p_1^2+p^2-2p_1p\cos\left(p_1;p\right)}=....\Rightarrow v_2=\dfrac{p_2}{m_2}\) Thay số vào nốt là xong bạn
\(\cos\left(p_2;p\right)=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}=.....\)
b) Mảnh nhỏ bay lên theo phương thẳng đứng cho ta hình dạng của 1 tam giác vuông
\(p_2=\sqrt{p^2+p_1^2}=\sqrt{\left(mv\right)^2+\left(m_1v_1\right)^2}=...\) \(\Rightarrow v_2=\dfrac{p_2}{m_2}=.....\) (....bạn tự tính điền vào )
\(\cos\left(p_2;p\right)=\dfrac{p}{p_2}=......\) tính nốt :D
Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Lời giải
Ta có:
+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
+ Gọi m 1 = 0 , 6 m là khối lượng của mảnh thứ nhất
=> Khối lượng của mảnh còn lại là m 2 = m − m 1 = m − 0 , 6 m = 0 , 4 m
+ Áp dụng định luật bảo toàn động lượng ta có: p → = p → 1 + p → 2
m v → = m 1 v → 1 + m − m 1 v → 2
Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ
=> v → 1 ↑ ↑ v →
Ta suy ra:
v 2 = m v − m 1 v 1 m − m 1 = ( 10 − 25.0 , 6 ) m ( 1 − 0 , 6 ) m = − 12 , 5 m / s
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Đáp án: B
Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
a) Áp dụng định luật bảo toàn động lượng:
chiều (+) là chiều chuyển động của đạn:
\(0=Mv+mv_0\Rightarrow v=-4\left(m/s\right)\)
=> khẩu pháo chuyển động ngược chiều đạn bay.
b) \(MV=Mv+mv_o\Rightarrow v=1\left(m/s\right)\)
=> Khẩu pháo chuyển động cùng chiều đạn bay.
c) \(-MV=Mv+mv_o\Rightarrow v=-9\left(m/s\right)\)
=> Khẩu pháo chuyển động ngược chiều đạn bay.
Chú thích: V là vận tốc khẩu pháo trước bắn. v là vận tốc khẩu pháo sau bắn và vo là vận tốc viên đạn khi ra khỏi nòng pháo.
b,c của cậu sai r kìa !!! lúc chưa bắn phải cộng thêm khối lượng của viên đạn nữa :))
Bỏ qua ma sát hệ là kín theo phương ngang áp dụng định luật bảo toàn động lượng:
\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=\left(m_1+m_2\right)\overrightarrow{v}\left(1\right)\)
Chọn chiều (+) là chiều chuyển động của m1
a) (1) => \(m_1v_1+m_2v_2=\left(m_1+m_2\right)v\Rightarrow v=\dfrac{m_1v_1+m_2v_2}{m_1+m_2}=\dfrac{4}{3}\left(m/s\right)\)
vật sau va chạm chuyển động cùng chiều (+)
b) (1) => \(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\Rightarrow v=\dfrac{m_1v_1-m_2v_2}{m_1+m_2}=\dfrac{2}{3}\left(m/s\right)\)
vật sau va chạm chuyển động cùng chiều (+)
Thể tích của hòn đá là
100-55=45(cm^3)
b)đổi
120g=0,12kg
Vì P=10m
=>trọng lượng của hòn đá là
0,12 x 10=1,2(N)
c)Vì \(m_2=2m_1\)
=>\(V_2=2V_1\)
Khối lượng quả cầu thứ 2 là
2 x 45=90(m^3)
Khối lượng nước tăng lên
55+90=145(m^3)
Tickk nha
Chọn D.
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng:
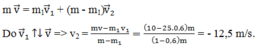
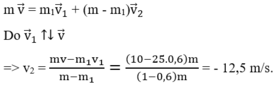
Ban tu ve hinh nhe? :D
Hệ kín động lượng được bảo toàn. \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Ta có: \(\left\{{}\begin{matrix}p=mv=250m\left(kg.m/s\right)\\p_1=\dfrac{m}{2}.v_1=125m\left(kg.m/s\right)\end{matrix}\right.\)
Áp dụng định lý hàm cos ta có:
\(\cos\alpha=\dfrac{p^2+p_1^2-p_2^2}{2p_1p}=\dfrac{250^2m^2+125^2m^2-\dfrac{m^2}{4}v_2^2}{2.250m.125m}\)
\(\Leftrightarrow250.125=250^2+125^2-\dfrac{1}{4}v_2^2\) \(\Rightarrow v_2=\sqrt{187500}\left(m/s\right)\simeq433\left(m/s\right)\)
Gọi \(\beta\) là góc hợp bởi mảnh 2 và phương thẳng đứng:
\(\cos\beta=\dfrac{p^2+p_2^2-p_1^2}{2p_2p}=\dfrac{250^2+216,5^2-125^2}{2.250.216,5}=0,86\)
\(\Rightarrow\beta\simeq31^0\)